题目内容
在极坐标系中,O为极点,半径为2的圆C的圆心的极坐标为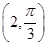 .
.
(1)求圆C的极坐标方程;
(2)P是圆C上一动点,点Q满足3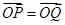 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
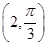 .
.(1)求圆C的极坐标方程;
(2)P是圆C上一动点,点Q满足3
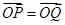 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.(1)ρ=4cos (2)x2+y2-6x-6
(2)x2+y2-6x-6 y=0
y=0
 (2)x2+y2-6x-6
(2)x2+y2-6x-6 y=0
y=0(1)设M(ρ,θ)是圆C上任一点,过点C作CH⊥OM于H点,则在Rt△COH中,OH=OC·cos∠COH.
∵∠COH=∠COM=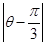 ,OH=
,OH= OM=
OM= ρ,
ρ,
OC=2,∴ ρ=2cos
ρ=2cos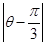 ,
,
即ρ=4cos 为所求的圆C的极坐标方程.
为所求的圆C的极坐标方程.
(2)设点Q的极坐标为(ρ,θ),∵33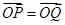 ,
,
∴P的极坐标为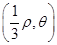 ,
,
代入圆C的极坐标方程得 ρ=4cos
ρ=4cos  ,
,
即ρ=6cos θ+6 sin θ,
sin θ,
∴ρ2=6ρcos θ+6 ρsin θ,令x=ρcos θ,y=ρsin θ,
ρsin θ,令x=ρcos θ,y=ρsin θ,
得x2+y2=6x+6 y,
y,
∴点Q的轨迹的直角坐标方程为x2+y2-6x-6 y=0.
y=0.
∵∠COH=∠COM=
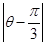 ,OH=
,OH= OM=
OM= ρ,
ρ,OC=2,∴
 ρ=2cos
ρ=2cos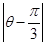 ,
,即ρ=4cos
 为所求的圆C的极坐标方程.
为所求的圆C的极坐标方程.(2)设点Q的极坐标为(ρ,θ),∵33
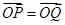 ,
,∴P的极坐标为
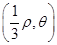 ,
,代入圆C的极坐标方程得
 ρ=4cos
ρ=4cos  ,
,即ρ=6cos θ+6
 sin θ,
sin θ,∴ρ2=6ρcos θ+6
 ρsin θ,令x=ρcos θ,y=ρsin θ,
ρsin θ,令x=ρcos θ,y=ρsin θ,得x2+y2=6x+6
 y,
y,∴点Q的轨迹的直角坐标方程为x2+y2-6x-6
 y=0.
y=0.
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
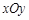 中,圆的参数方程为
中,圆的参数方程为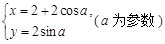 ,以坐标原点
,以坐标原点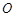 为极点,
为极点,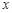 轴的正半轴为极轴建立极坐标系.求:
轴的正半轴为极轴建立极坐标系.求: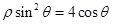 ,直线
,直线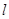 的参数方程为
的参数方程为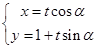 (t为参数,
(t为参数,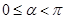 )
) 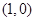 ,求直线
,求直线 中,已知直线
中,已知直线 的参数方程是
的参数方程是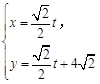 (
(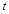 为参数);以
为参数);以 为极点,
为极点, 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆 的极坐标方程为
的极坐标方程为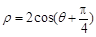 .由直线
.由直线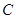 的极坐标方程为
的极坐标方程为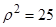 ,曲线
,曲线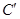 的极坐标方程为
的极坐标方程为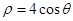 .试求曲线
.试求曲线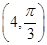 ,求|CP|.
,求|CP|.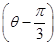 =a,a∈R,圆C的参数方程是
=a,a∈R,圆C的参数方程是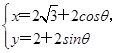 (θ为参数).若圆C关于直线l对称,则a=________.
(θ为参数).若圆C关于直线l对称,则a=________.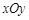 中,以原点
中,以原点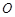 为极点,
为极点,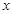 轴的正半轴为极轴建立极坐标系.若曲线
轴的正半轴为极轴建立极坐标系.若曲线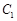 的参数方程为
的参数方程为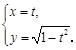 (
(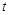 为参数),曲线
为参数),曲线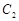 的极坐标方程为
的极坐标方程为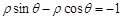 .则曲线
.则曲线