题目内容
【题目】已知点![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是抛物线上的定点,且
是抛物线上的定点,且![]() .
.
![]() 求抛物线
求抛物线![]() 的方程;
的方程;
![]() 直线
直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() ,
,![]() ,直线AB与切线l平行,设切点为N点,试问
,直线AB与切线l平行,设切点为N点,试问![]() 的面积是否是定值,若是,求出这个定值;若不是,请说明理由.
的面积是否是定值,若是,求出这个定值;若不是,请说明理由.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)设出点M和F的坐标,根据向量坐标化得到![]() ,进而得到点M的坐标,代入抛物线可得到方程;(2)
,进而得到点M的坐标,代入抛物线可得到方程;(2)![]() 的中点为
的中点为![]() ,联立直线AB和抛物线方程,得到
,联立直线AB和抛物线方程,得到![]() ,联立切线和抛物线得到切点
,联立切线和抛物线得到切点![]() 的坐标为
的坐标为![]() ,
,![]() ,进而得到轴,
,进而得到轴,![]() ,结合
,结合![]() 得到
得到![]() ,
,![]() .
.
![]() 设
设![]() ,由题知
,由题知![]() ,
,
所以![]()
所以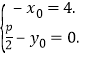 即
即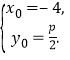
代入![]() 中得
中得![]() ,解得
,解得![]()
所以抛物线![]() 的方程为
的方程为![]()
![]() 有题意知,直线
有题意知,直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]()
由![]() 消去
消去![]() ,整理得
,整理得![]()
则![]()
![]()
设![]() 的中点为
的中点为![]() ,
,
则点![]() 的坐标为
的坐标为![]()
由条件设切线方程为![]()
由![]() 消去
消去![]() ,整理得
,整理得![]()
![]() 直线与抛物线相切,
直线与抛物线相切,
![]() .
.
![]()
![]()
![]() 切点
切点![]() 的坐标为
的坐标为![]() ,
,
![]() 轴,
轴,![]()
![]()
又![]()
![]()
![]()
![]() 的面积为定值,且定值为
的面积为定值,且定值为![]() .
.

练习册系列答案
相关题目
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量![]() 单位:万只
单位:万只![]() 与相应年份
与相应年份![]() 序号
序号![]() 的数据表和散点图
的数据表和散点图![]() 如图所示
如图所示![]() ,根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数
,根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数![]() 单位:个
单位:个![]() 关于x的回归方程
关于x的回归方程![]() .
.
年份序号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
年养殖山羊 |
|
|
|
|
|
|
|
|
|
![]() 根据表中的数据和所给统计量,求y关于x的线性回归方程
根据表中的数据和所给统计量,求y关于x的线性回归方程![]() 参考统计量:
参考统计量:![]() ,
,![]() ;
;
![]() 试估计:
试估计:![]() 该县第一年养殖山羊多少万只
该县第一年养殖山羊多少万只
![]() 到第几年,该县山羊养殖的数量与第一年相比缩小了?
到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.