题目内容
若函数f（x）=ax+1在区间（-1，1）上存在一个零点，则实数a的取值范围是（ ）
| A、a＞1 | B、a＜1 | C、a＜-1或a＞1 | D、-1＜a＜1 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：由函数的零点的判定定理可得f（-1）f（1）＜0，解不等式求得实数a的取值范围．
解答：解：函数f（x）=ax+1在区间（-1，1）上存在一个零点，则f（-1）f（1）＜0，即 （1-a）（1+a）＜0，解得a＜-1或a＞1．
故选：C．
故选：C．
点评：本题主要考查函数的零点的判定定理的应用，属于基础题．
练习册系列答案
相关题目
已知全集为R，集合A={y|y=2x}，B={x|log2x＞0}，则（ ）
| A、A∪B=R | B、A∩B=A | C、A∪（∁RB）=R | D、（∁RA）∪B=R |
下列函数中图象关于原点中心对称的是（ ）
| A、y=x2+1 | B、y=x，x∈（-1，1] | C、y=x3 | D、y=x+1 |
函数y=loga（x-1）+2（a＞0，a≠1）的图象恒过点（ ）
| A、（1，2） | B、（2，2） | C、（2，3） | D、（4，4） |
已知函数f（x）=x2014（x∈R），又α、β是锐角三角形的两个内角，则有（ ）
| A、f（sinα）＞f（cosβ） | B、f（sinα）＜f（cosβ） | C、f（sinα）＞f（sinβ） | D、f（cosα）＞f（cosβ） |
设f（x）=lnx-
，若f（x）在（2，3）内有唯一零点，则实数a的取值范围是（ ）
| a |
| x |
A、
| ||||||||
B、（
| ||||||||
| C、（2ln2，3ln3） | ||||||||
| D、（2ln2，3ln3）∪（-3ln3，-2ln2） |
已知函数f（x）=
，那么不等式f（x）≥1的解集为（ ）
|
| A、{x|-3≤x≤0} |
| B、{x|x≤-3或x≥0} |
| C、{x|0≤x≤3} |
| D、{x|x≤0或x≥3} |
已知函数f（x）=
，若f（a）=1，则a的所有可能结果之和为（ ）
|
| A、e | ||
B、
| ||
C、e+
| ||
D、2e+
|
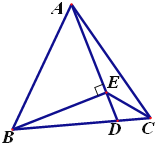如图，△ABC是边长为2的等边三角形，D是边BC上的动点，BE⊥AD于E，则CE的最小值为（ ）| A、1 | ||||
B、2-
| ||||
C、
| ||||
D、
|