Question

已知函数y=f(x)是定义在区间［-，］上的偶函数，且x∈［0，］时，f（x）=-x²-x+5.（1）求函数f(x)的解析式；

（2）若矩形ABCD的顶点A，B在函数y=f(x)的图象上，顶点C，D在x轴上，求矩形ABCD面积的最大值.

Answer 1

（1）f(x)=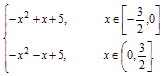（2）当t=1时，矩形ABCD的面积取得极大值6，且此极大值也是S（t）在t∈（0，］上的最大值，从而当t=1时，矩形ABCD的面积取得最大值6.

解析:

（1）当x∈［-，0］时，-x∈［0，］.

∴f(-x)=-(-x)²-(-x)+5=-x²+x+5.

又∵f(x)是偶函数，

∴f（x）=f(-x)=-x²+x+5.

∴f(x)=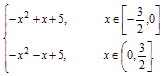

（2）由题意，不妨设A点在第一象限，坐标为（t,-t²-t+5）,其中t∈（0，］.

由图象对称性可知B点坐标为（-t，-t²-t+5）.则S(t)=S_矩形ABCD=2t（-t²-t+5）=-2t³-2t²+10t.

=-6t²-4t+10.由=0，得t₁=-（舍去），t₂=1.当0＜t＜1时， ＞0;t＞1时, ＜0.

∴S(t)在（0，1］上单调递增，在［1，］上单调递减.∴当t=1时，矩形ABCD的面积取得极大值6，且此极大值也是S（t）在t∈（0，］上的最大值，从而当t=1时，矩形ABCD的面积取得最大值6.