题目内容
设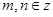 ,已知函数
,已知函数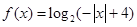 的定义域是
的定义域是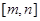 ,值域是
,值域是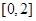 ,若函数
,若函数
g(x)=2︱x-1︱+m+1有唯一的零点,则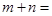 ( )
( )
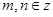 ,已知函数
,已知函数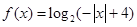 的定义域是
的定义域是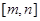 ,值域是
,值域是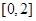 ,若函数
,若函数g(x)=2︱x-1︱+m+1有唯一的零点,则
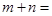 ( )
( )| A.2 | B.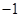 | C.1 | D.0 |
C
专题:计算题.
分析:由关于x的方程2|x-1|+m+1=0有唯一的实数解,我们易得m的值,然后根据函数f(x)=log2(-|x|+4)的定义域是[m,n],值域是[0,2],结合函数f(x)=log2(-|x|+4)的性质,可求出n的值,进而得到答案.
解答:解:∵f(x)=log2(-|x|+4)的值域是[0,2],
∴(-|x|+4)∈[1,4]
∴-|x|∈[-3,0]
∴|x|∈[0,3]…①
若若关于x的方程2|x-1|+m+1=0有唯一的实数解
则m=-2
又由函数f(x)=log2(-|x|+4)的定义域是[m,n],
结合①可得n=3
即:m+n=1
故选C
点评:本题考查的知识点是根的存在性及根的个数的判断,对数函数的定义域及对数函数的值域,其中利用关于x的方程2|1-x|+m+1=0有唯一的实数解,变形得到关于x的方程2|1-x|+1=-m有唯一的实数解,即-m为函数y=2|1-x|+1的最值,是解答本题的关键.

练习册系列答案
相关题目
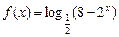 的定义域为
的定义域为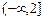 。
。 的值域;
的值域;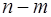 表示
表示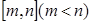 的区间长度,函数
的区间长度,函数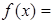
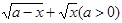 的值域区间长度为
的值域区间长度为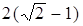 ,则实数
,则实数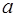 的值是( )
的值是( )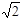
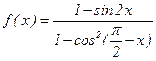
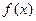 的定义域; (2)已知
的定义域; (2)已知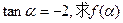 的值.
的值. =
= ,其中
,其中 表示不超过x的最大整数,
表示不超过x的最大整数,  =1,
=1, =-2.当x∈
=-2.当x∈ ,
, (n∈
(n∈ )时,设函数
)时,设函数 ,则式子
,则式子 的最小值为 .
的最小值为 .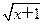 的定义域为M,集合N={y|y=
的定义域为M,集合N={y|y=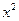 ,x∈R},则M∩N=
,x∈R},则M∩N=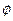
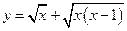 的定义域为
的定义域为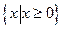
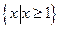
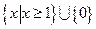
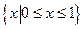
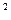 +bx+3a+b为偶函数,其定义域为 [ a—1, 2a ],则函数的值域为 。
+bx+3a+b为偶函数,其定义域为 [ a—1, 2a ],则函数的值域为 。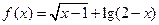 的定义域为 .
的定义域为 .