题目内容
若函数y=f(x)(x∈R)满足f(x+1)=f(x-1),且x∈[-1,1]时,f(x)=1-x2,函数g(x)= 则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )
则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )
| A.6 | B.7 | C.8 | D.9, |
C
解析

练习册系列答案
相关题目
设a为实数,函数f(x)=x3+ax2+(a-2)x的导数是f′(x),且f′(x)是偶函数,则曲线y=f(x)在原点处的切线方程为( )
| A.y=-2x | B.y=3x |
| C.y=-3x | D.y=4x |
已知函数f(x)的图像如图所示,则f(x)的解析式可以是( )
A.f(x)=x- | B.f(x)= | C.f(x)= -1 -1 | D.f(x)= |
已知函数f(x)是R上的单调递增函数且为奇函数,数列{an}是等差数列,a3>0,则f(a1)+f(a3)+f(a5)的值( )
| A.恒为正数 |
| B.恒为负数 |
| C.恒为0 |
| D.可以为正数也可以为负数 |
若关于x的方程x2+mx+1=0有两个不相等的实数根,则实数m的取值范围是 ( ).
| A.(-1,1) | B.(-2,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-∞,-1)∪(1,+∞) |
已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)= ,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围是( ).
,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围是( ).
A.0<k≤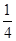 或k= 或k= | B.0<k≤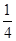 |
C.0<k<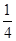 或k= 或k= | D.0<k<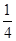 |
 的图象大致是( )
的图象大致是( )
 表示不超过
表示不超过 的最大整数,例如:[3.1]=3,[
的最大整数,例如:[3.1]=3,[ 2.6]=
2.6]= 是函数
是函数 导函数,设
导函数,设 ,则函数
,则函数 的值域是( )
的值域是( )



 的对角线
的对角线 上任取一点P,以
上任取一点P,以 为球心,
为球心, 为半径作一个球.设
为半径作一个球.设 ,记该球面与正方体表面的交线的长度和为
,记该球面与正方体表面的交线的长度和为 ,则函数
,则函数