题目内容
(本题满分12分)某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: ,
, ,…,
,…, 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
(1)求图中实数 的值;
的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级
期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在 与
与 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
(1)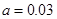 (2)544(3)
(2)544(3)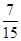
解析试题分析:(1)由于图中所有小矩形的面积之和等于1,
所以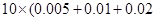
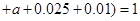 . ……2分
. ……2分
解得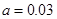 . ……3分
. ……3分
(2)根据频率分布直方图,成绩不低于60分的频率
为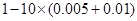
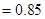 . ……5分
. ……5分
由于该校高一年级共有学生640人,利用样本估计总体的思想,
可估计该校高一年级数学成绩不低于60分的人数约为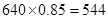 人. ……6分
人. ……6分
(3)成绩在 分数段内的人数为
分数段内的人数为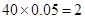 人,分别记为
人,分别记为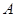 ,
,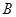 . ……7分
. ……7分
成绩在 分数段内的人数为
分数段内的人数为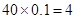 人,分别记为
人,分别记为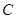 ,
,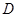 ,
,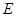 ,
,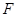 . ……8分
. ……8分
若从数学成绩在 与
与 两个分数段内的学生中随机选取两名学生,
两个分数段内的学生中随机选取两名学生,
则所有的基本事件有: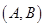 ,
,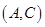 ,
,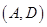 ,
,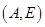 ,
,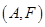 ,
,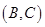 ,
,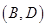 ,
,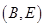 ,
,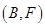 ,
,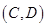 ,
,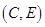 ,
,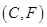 ,
,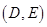 ,
,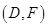 ,
,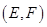 共15种. ……10分
共15种. ……10分
如果两名学生的数学成绩都在 分数段内或都在
分数段内或都在 分数段内,那么这两名学生的数学成绩之差的绝对值一定不大于10.如果一个成绩在
分数段内,那么这两名学生的数学成绩之差的绝对值一定不大于10.如果一个成绩在 分数段内,另一个成绩在
分数段内,另一个成绩在 分数段内,那么这两名学生的数学成绩之差的绝对值一定大于10.
分数段内,那么这两名学生的数学成绩之差的绝对值一定大于10.
记“这两名学生的数学成绩之差的绝对值不大于10”为事件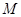 ,则事件
,则事件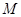 包含的基本事件有:
包含的基本事件有: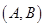 ,
,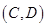 ,
,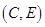 ,
,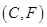 ,
,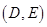 ,
,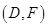 ,
,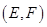 共7种. ……11分
共7种. ……11分
所以所求概率为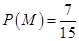 . ……12分
. ……12分
考点:本小题主要考查频率分布直方图的应用和古典概型概率的求解,考查学生识图、用图的能力和运算求解能力.
点评:解决与频率分布直方图有关的题目时,要注意到频率分布直方图中纵轴表示的是
频率/组距,不是频率,图中小矩形的面积才表示频率.

 阅读快车系列答案
阅读快车系列答案
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个至多一个“成绩优秀”的概率;
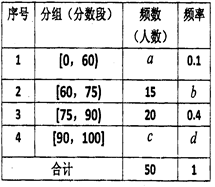
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
| | 甲班 (A方式) | 乙班 (B方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |

 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2. 706 | 3. 841 | 5. 024 |
(10分)某种产品的广告费支出x与消费额y(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)预测当广告费支出为700万元时的销售额.
某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了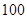 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
| | 数学 | 语文 | 总计 |
| 初中 | 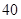 | 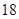 | 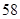 |
| 高中 | 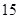 | 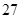 | 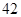 |
| 总计 | 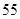 | 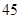 | 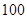 |
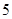 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?(2) 在(1)中抽取的
 名学生中任取
名学生中任取 名,求恰有
名,求恰有 名初中学生的概率.
名初中学生的概率. 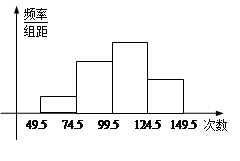
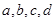 的值;
的值; ,
, ,…,
,…, 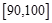 后得到如下频率分布直方图.
后得到如下频率分布直方图.
 内的频率;
内的频率;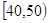 ,
,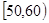 …
…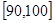 后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题:
后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题: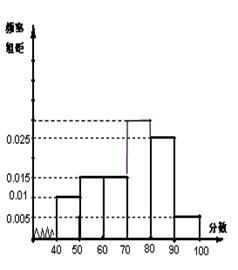
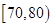 的频率.
的频率.