题目内容
对于有限数列A:{a1,a2,a3,…,an}Si为数列A的前i项和,称
(S1+S2+S3+…+Sn)为数列A的“平均和”,将数字1,2,3,4,5,6,7任意排列,所对应数列的“平均和”的最大值是( )
| 1 |
| n |
分析:要使得所求的平均和最大,只要7出现的最多,1出现的最少,根据题意可知将数字1,2,3,4,5,6,7的排列为7,6,5,4,3,2,1时,符合题意,可求
解答:解:根据题意可知,将数字1,2,3,4,5,6,7的排列为7,6,5,4,3,2,1时,,所对应数列的“平均和”最大
此时
(S1+S2+…+S7)=
[7+(7+6)+(7+6+5)+…+(7+6+5+4+3+2+1)]
=
(7×7+6×6+5×5+…+1×1)
=
=20
故答案为:20
此时
| 1 |
| 7 |
| 1 |
| 7 |
=
| 1 |
| 7 |
=
| 49+36+25+16+9+4+1 |
| 7 |
故答案为:20
点评:本题以新定义为载体,主要考查了数列的求和,解题的关键是寻求满足条件的排列方式

练习册系列答案
相关题目
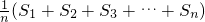 为数列A的“平均和”,将数字1,2,3,4,5,6,7任意排列,所对应数列的“平均和”的最大值是
为数列A的“平均和”,将数字1,2,3,4,5,6,7任意排列,所对应数列的“平均和”的最大值是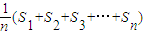 为数列A的“平均和”,将数字1,2,3,4,5,6,7任意排列,所对应数列的“平均和”的最大值是( )
为数列A的“平均和”,将数字1,2,3,4,5,6,7任意排列,所对应数列的“平均和”的最大值是( )