题目内容
【题目】已知函数f(x)是定义域为R的偶函数,当![]() 时,f(x)=x2-2x
时,f(x)=x2-2x

(1)求出函数f(x)在R上的解析式;
(2)画出函数f(x)的图象,并根据图象写出f(x)的单调区间.
(3)求使f(x)=1时的x的值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1) 设![]() ,则
,则![]() ,根据函数
,根据函数![]() 为
为![]() 上的偶函数,当
上的偶函数,当![]() 时
时![]() ,可得函数解析式;(2)根裾函数的解折式,利用描点法结合对称性可得函数的图象,利用函数的图象,可得函数的单谓区间;(3)结合
,可得函数解析式;(2)根裾函数的解折式,利用描点法结合对称性可得函数的图象,利用函数的图象,可得函数的单谓区间;(3)结合![]() 的范围,分两种情况解方程可得到
的范围,分两种情况解方程可得到![]() 的值.
的值.
(1)当x<0时,-x>0,因为f(x)是偶函数,所以f(-x)=f(x).
所以f(x)=f(-x)=x2+2x.
综上:f(x)=![]() .
.
(2)图象如图所示.
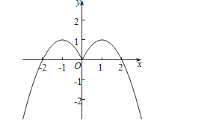
由图可知,单调增区间:[-1,0],[1,+∞)
单调减区间:(-![]() ,-1),(0,1).
,-1),(0,1).
(3)当x>0时,x2-2x=1
解得![]()
因为x>0,所以![]()
当x<0时,x2+2x=1,解得x=-1-![]() 或
或![]() ,
,
因为x<0,所以x=-1-![]()
综上所述,![]()

练习册系列答案
相关题目
