题目内容
【题目】已知椭圆![]() ,过
,过![]() 上一点
上一点![]() 的切线
的切线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设过点![]() 且斜率不为
且斜率不为![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,试问
两点,试问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得 ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(Ⅰ)![]() (Ⅱ)存在点
(Ⅱ)存在点![]() 使得
使得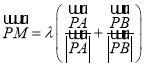 .
.
【解析】试题分析: (I)由直线与椭圆相切,联立方程,有且只有两个相同的实数根,求出![]() 之间的一个关系式,再根据点
之间的一个关系式,再根据点![]() 在椭圆上,求出
在椭圆上,求出![]() 的值,得出椭圆方程;(II)联立直线AB的方程与椭圆方程,求出两根之和,两根之积的表达式,由已知得出PM平分
的值,得出椭圆方程;(II)联立直线AB的方程与椭圆方程,求出两根之和,两根之积的表达式,由已知得出PM平分![]() ,得出直线PA与PB倾斜角互补,它们的斜率和为零,求出
,得出直线PA与PB倾斜角互补,它们的斜率和为零,求出![]() 的值.
的值.
试题解析:(Ⅰ)由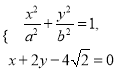 消去
消去![]() 并整理得
并整理得
![]() .
.
∵椭圆![]() 与直线
与直线![]() 相切,
相切,
∴![]() ,
,
化简得![]() ,①
,①
又点![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() .②
.②
由①②得![]() ,
, ![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)存在.理由如下:
设直线![]() 的方程为
的方程为![]() ,
,
联立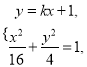 消去
消去![]() 并整理得
并整理得![]() .
.
![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
假设存在点![]() 满足条件,
满足条件,
由于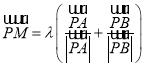 ,所以
,所以![]() 平分
平分![]() .
.
易知直线![]() 与直线
与直线![]() 的倾斜角互补,∴
的倾斜角互补,∴![]() ,
,
即![]() ,即
,即![]() .(
.(![]() )
)
将![]() ,
, ![]() 代入(
代入(![]() )并整理得
)并整理得
![]() ,
,
∴![]() ,
,
整理得![]() ,即
,即![]() ,
,
∴当![]() 时,无论
时,无论![]() 取何值均成立.
取何值均成立.
∴存在点![]() 使得
使得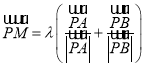 .
.
点睛: 本题主要考查了求椭圆方程等相关知识,属于中档题. 本题路: (I)由直线与椭圆相切,联立直线与椭圆方程,消去![]() ,得到一个关于
,得到一个关于![]() 的一元二次方程,判别式为零,得到
的一元二次方程,判别式为零,得到![]() 之间的一个关系式, 再根据点
之间的一个关系式, 再根据点![]() 在椭圆上,求出
在椭圆上,求出![]() 的值,得出椭圆方程;(II)设直线AB的方程为
的值,得出椭圆方程;(II)设直线AB的方程为![]() ,联立直线与椭圆方程, 消去
,联立直线与椭圆方程, 消去![]() ,得到一个关于
,得到一个关于![]() 的一元二次方程,求出两根之和,两根之积的表达式,由向量之间的关系得出PM平分
的一元二次方程,求出两根之和,两根之积的表达式,由向量之间的关系得出PM平分![]() ,所以
,所以![]() , 求出
, 求出![]() 的值.
的值.

练习册系列答案
相关题目