题目内容
【题目】已知函数![]() (a<0).
(a<0).
(Ⅰ)当a=-3时,求f(x)的单调递减区间;
(Ⅱ)若函数f(x)有且仅有一个零点,求实数a的取值范围;
【答案】(1) 单调递减区间为(-3,-2)和(0,+∞);(2) a<0.
【解析】试题分析:(1)解关于导函数的不等式,得到所求的单调减区间;(2)函数f(x)有且仅有一个零点,即函数图象与x轴有唯一的公共点,利用导函数研究函数图象走势即可.
试题解析:
(Ⅰ)∵a=-3,∴![]() ,故
,故![]()
令f′(x)<0,解得-3<x<-2或x>0,
即所求的单调递减区间为(-3,-2)和(0,+∞)
(Ⅱ)∵![]() (x>a)
(x>a)
令f′(x)=0,得x=0或x=a+1
(1)当a+1>0,即-1<a<0时,f(x)在(a,0)和(a+1,+∞)上为减函数,在(0,a+1)上为增函数.
由于f(0)=aln(-a)>0,当x→a时,f(x)→+∞.
当x→+∞时,f(x)→-∞,于是可得函数f(x)图像的草图如图,
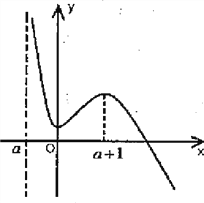
此时函数f(x)有且仅有一个零点.
即当-1<a<0对,f(x)有且仅有一个零点;
(2)当a=-1时,![]() ,
,
∵![]() ,∴f(x)在(a,+∞)单调递减,
,∴f(x)在(a,+∞)单调递减,
又当x→-1时,f(x)→+∞.当x→+∞时,f(x)→-∞,
故函数f(x)有且仅有一个零点;
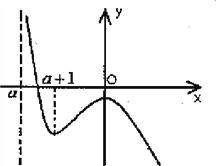
(3)当a+1<0即a<-1时,f(x)在(a,a+1)和(0,+∞)上为减函数,在(a+1,0)上为增函数.又f(0)=aln(-a)<0,当x→a时,f(x)→+∞,当x→+∞时,f(x)→-∞,于是可得函数f(x)图像的草图如图,此时函数f(x)有且仅有一个零点;
综上所述,所求的范围是a<0.

 计算高手系列答案
计算高手系列答案【题目】某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x元与日销售量y件之间有如下所表示的关系.
x | … | 30 | 40 | 45 | 50 | … |
y | … | 60 | 30 | 15 | 0 | … |
(1)在所给的坐标系中,如图,根据表格提供的数据描出实数对(x,y)的对应点,并确定y与x的一个函数关系式y=f(x);
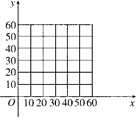
(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少时,才能获得最大日销售利润?