题目内容
19．化简：（1）cos（2α+β）+2sin（α+β）sinα；
（2）$\frac{cos7°-sin15°sin8°}{cos8°}$．
分析 利用“和差公式”即可的．
解答 解：（1）cos（α+β）cosα-2sin（α+β）sinα+2sin（α+β）sinα=cos（α+β）cosα+sin（α+β）sinα=cos（α+β-α）=cosβ．
（2）原式=$\frac{cos（1{5}^{°}-{8}^{°}）-sin1{5}^{°}sin{8}^{°}}{cos{8}^{°}}$=$\frac{cos1{5}^{°}cos{8}^{°}}{cos{8}^{°}}$=cos15°=cos（45°-30°）=cos45°cos30°+sin45°sin30°=$\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}×\frac{1}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$．
点评 本题考查了“和差公式”的应用，考查了计算能力，属于基础题．
练习册系列答案
相关题目
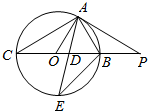如图，已知直线PA与⊙O切于点A，直线PB过圆心O，且与⊙O交于点B、C（PB＜PC），若PA=3，PB=1．