题目内容
【题目】已知
，现给出如下结论：
①
； ②
； ③
； ④
.
其中正确结论的序号为（ ）
A. ②③ B. ①④ C. ②④ D. ①③
【答案】A
【解析】分析：先求出f′（x），再进行因式分解，求出f′（x）＜0和f′（x）＞0对应x的范围，即求出函数的单调区间和极值，再由条件判断出a、b、c的具体范围和f（1）＞0且f（2）＜0，进行求解得到abc的符号，进行判断出f（0）的符号．
详解：由题意得，f′（x）=3x2﹣9x+6=3（x﹣1）（x﹣2），
∴当x＜1或x＞2时，f′（x）＞0，当1＜x＜2时，f′（x）＜0，
∴函数f（x）的增区间是（﹣∞，1），（2，+∞），减区间是（1，2），
∴函数的极大值是f（1）=
，函数的极小值是f（2）=2﹣abc，
∵a＜b＜c，且f（a）=f（b）=f（c）=0，
∴a＜1＜b＜2＜c，f（1）＞0且f（2）＜0，解得2＜
，
∴f（0）=﹣abc＜0，
则f（0）f（1）＜0、f（0）f（2）＞0，
故答案为：A．
【题目】为了了解我市特色学校的发展状况，某调查机构得到如下统计数据：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
（Ⅰ）根据上表数据，计算
与
的相关系数
，并说明与的线性相关性强弱（已知：
，则认为与线性相关性很强；
，则认为与线性相关性一般；
，则认为与线性相关性较弱）；
（Ⅱ）求关于的线性回归方程，并预测我市2019年特色学校的个数（精确到个）．
参考公式：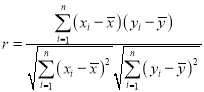 
，
，
，
，
，
．
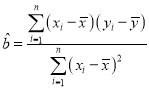【题目】为了评估A，B两家快递公司的服务质量，从两家公司的客户中各随机抽取100名客户作为样本，进行服务质量满意度调查，将A，B两公司的调查得分分别绘制成频率分布表和频率分布直方图．规定
分以下为对该公司服务质量不满意．
分组 | 频数 | 频率 |
|
|
|
|
|
|
|
| 0.4 |
|
|
|
|
|
|
合计 |
|
|
（Ⅰ）求样本中对B公司的服务质量不满意的客户人数；
（Ⅱ）现从样本对A，B两个公司服务质量不满意的客户中，随机抽取2名进行走访，求这两名客户都来自于B公司的概率；
（Ⅲ）根据样本数据，试对两个公司的服务质量进行评价，并阐述理由．
【题目】对某校高三年级学生参加社区服务次数进行统计，随机抽取
名学生作为样本，得到这名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图：
分组 | 频数 | 频率 |
|
|
|
| 24 |
|
| 4 | 0.1 |
| 2 | 0.05 |
合计 |
| 1 |
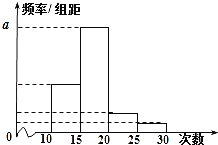
（1）求出表中，
及图中
的值；
（2）若该校高三学生有240人，试估计该校高三学生参加社区服务的次数在区间
内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间
内的概率．