题目内容
【题目】如图,曲线![]() 由曲线
由曲线![]() 和曲线
和曲线![]() 组成,其中点
组成,其中点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点.
所在圆锥曲线的焦点.
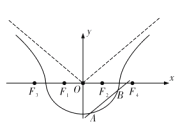
(Ⅰ)若![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅱ)如图,作直线![]() 平行于曲线
平行于曲线![]() 的渐近线,交曲线于点
的渐近线,交曲线于点![]() ,求证:弦
,求证:弦![]() 的中点
的中点![]() 必在曲线
必在曲线![]() 的另一条渐进线上;
的另一条渐进线上;
(Ⅲ)对于(Ⅰ)中的曲线![]() ,若直线
,若直线![]() 过点
过点![]() 交曲线
交曲线![]() 于点
于点![]() ,求
,求![]() 与
与![]() 面积之和的最大值.
面积之和的最大值.
【答案】(Ⅰ)![]() 和
和![]() ;(Ⅱ)证明见解析;(Ⅲ)
;(Ⅱ)证明见解析;(Ⅲ)![]() .
.
【解析】
试题分析:(1)由已知条件布列关于![]() 的方程组,即可得到曲线
的方程组,即可得到曲线![]() 的方程;(2)设直线
的方程;(2)设直线![]() 代入
代入![]() ,得到
,得到![]() ,从而可得
,从而可得![]() ,所以弦
,所以弦![]() 的中点
的中点![]() 必在曲线
必在曲线![]() 的另一条渐进线上;(3)由题意可知:
的另一条渐进线上;(3)由题意可知:![]() 和
和![]() 面积之和等于
面积之和等于![]() 面积的两倍,利用设而不求法表示
面积的两倍,利用设而不求法表示![]() ,整体换元结合均值不等式即可求得面积的最大值.
,整体换元结合均值不等式即可求得面积的最大值.
试题解析:
(Ⅰ)![]() ,
,
则曲线的方程为![]() 和
和![]()
(Ⅱ)曲线![]() 的渐近线为
的渐近线为![]() ,如图,设直线
,如图,设直线![]() ,
,
则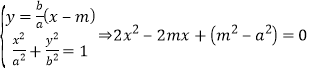 ,
,
设点![]() ,则
,则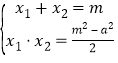 ,
,
![]() ,
,
![]() ,即点
,即点![]() 在直线
在直线![]() 上.
上.
(Ⅲ)因为![]() 的中点为原点
的中点为原点![]() ,所以
,所以![]() 和
和![]() 面积之和等于
面积之和等于![]() 面积的两倍,由(Ⅰ)知,曲线
面积的两倍,由(Ⅰ)知,曲线![]() ,点
,点![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
 ,
,
设![]() 由韦达定理:
由韦达定理: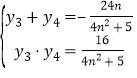 ,
,
所以![]() ,
,
![]() 到直线
到直线![]() 距离
距离![]() ,
,
![]() ,
,
令![]() ,
,
![]() ,
,
![]() ,当且仅当
,当且仅当![]() 即
即![]() 时等号成立,
时等号成立,
所以![]() 时,
时,![]()
![]() 与
与![]() 面积之和的最大值为
面积之和的最大值为![]()

练习册系列答案
相关题目
【题目】(2016·郑州模拟)某市公安局为加强安保工作,特举行安保项目的选拔比赛活动,其中A、B两个代表队进行对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式进行三场比赛,每场胜队得1分,负队得0分,设A队、B队最后所得总分分别为ξ,η,且ξ+η=3.
对阵队员 | A队队员胜 | A队队员负 |
A1对B1 |
|
|
A2对B2 |
|
|
A3对B3 |
|
|
(1)求A队最后所得总分为1的概率;
(2)求ξ的分布列,并用统计学的知识说明哪个队实力较强.