Question

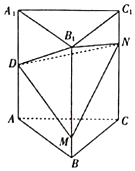
【题目】如图，在三棱柱ABC﹣A1B1C1中（底面△ABC为正三角形），A1A⊥平面ABC，AB=AC=2，，D是BC边的中点．

（1）证明：平面ADB1⊥平面BB1C1C．

（2）求点B到平面ADB1的距离．

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）证明AD⊥BC，BB1⊥AD，推出AD⊥平面BB1C1C，即可证明平面ADB1⊥平面BB1C1C;

（2）由，转化求解点B到平面ADB1的距离即可．

（1）∵AB=AC，D为BC的中点，

∴AD⊥BC．

又BB1⊥平面ABC，AD平面ABC，

∴BB1⊥AD．

又BC∩BB1=B，

∴AD⊥平面BB1C1C．

又AD平面ADB1，

∴平面ADB1⊥平面BB1C1C．

（2）由（1）知，AD⊥平面BB1C1C，B1D平面BB1C1C，

∴AD⊥B1D．，

∵，B1D=2，

∴，

．

设点B到平面ADB1的距离为d，

由，得，

即，

∴d，即点B到平面ADB1的距离为．