题目内容
8.在复平面内,复数z满足(2-i)•z=i3(i为虚数单位),则复数z表示的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 直接利用复数的代数形式的混合运算化简复数得到对应点,求解即可.
解答 解:复数z满足(2-i)•z=i3(i为虚数单位),
可得z=$\frac{-i}{2-i}$=$\frac{-i(2+i)}{(2-i)(2+i)}$=$\frac{1}{5}$$-\frac{2}{5}$i.复数对应点为($\frac{1}{5},-\frac{2}{5}$)在第三象限.
故选:C.
点评 本题考查复数的基本运算,复数的几何意义,基础题.

练习册系列答案
相关题目
19.不等式2kx2+kx-$\frac{3}{8}$<0对任何实数x恒成立,则k的取值范围是( )
| A. | (-3,0] | B. | (-3,0) | C. | [-3,0] | D. | [-3,0) |
13.若实数x,y满足$\left\{\begin{array}{l}{x+y≤3}\\{y≥2x}\\{x≥-1}\end{array}\right.$,则(x-3)2+y2的最小值是( )
| A. | $\frac{36}{5}$ | B. | 8 | C. | 20 | D. | 2$\sqrt{5}$ |
20.设实数x,y满足:$\left\{\begin{array}{l}{2x+y≤4}\\{x-2y≤2}\\{x-y≥1}\end{array}\right.$,O为坐标原点,则x2+y2的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
17.根据我国相关法律规定,食品的含汞量不得超过1.00ppm,沿海某市对一种贝类海鲜产品进行抽样检查,抽出样本20个,测得含汞量(单位:ppm)数据如下表所示:
(1)若从这20个产品汇总随机抽取3个,求恰有一个含汞量超标的概率;
(2)以此20个产品的样本数据来估计这批贝类海鲜产品的总体,若从这批数量很大的贝类海鲜产品中任选3个,记ξ表示抽到的产品含汞量超标的个数,求ξ的分布列及数学期望Eξ.
| 分组 | (0,0.25] | (0.25,0.50] | (0.50,0.75] | (0.75,1] | (1,1.25] | (1.25,1.5] |
| 数据 | 6 | 4 | 3 | 2 | 2 | 3 |
(2)以此20个产品的样本数据来估计这批贝类海鲜产品的总体,若从这批数量很大的贝类海鲜产品中任选3个,记ξ表示抽到的产品含汞量超标的个数,求ξ的分布列及数学期望Eξ.
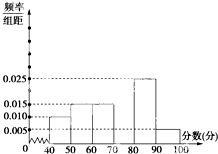 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: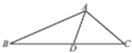 如图,在△ABC中,AB=3,AC=2,BC=4,点D在边BC上,∠BAD=30°,则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$.
如图,在△ABC中,AB=3,AC=2,BC=4,点D在边BC上,∠BAD=30°,则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$.