题目内容
设函数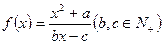 .若方程
.若方程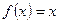 的根为
的根为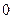 和
和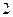 ,
,
且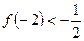 .
.
(1)求函数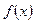 的解析式;
的解析式;
(2)已知各项均不为零的数列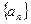 满足:
满足: 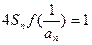 (
(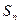 为该数列前
为该数列前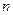 项和),求该数列的通项
项和),求该数列的通项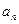 .
.
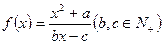 .若方程
.若方程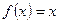 的根为
的根为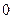 和
和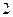 ,
,且
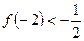 .
. (1)求函数
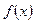 的解析式;
的解析式; (2)已知各项均不为零的数列
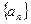 满足:
满足: 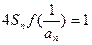 (
(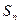 为该数列前
为该数列前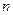 项和),求该数列的通项
项和),求该数列的通项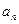 .
.⑴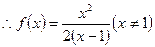 ⑵
⑵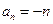
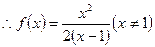 ⑵
⑵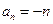
⑴设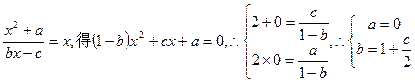
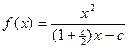 ,
,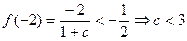 ,
,
又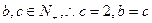
 ,
,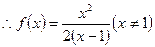
⑵由已知得
两式相减得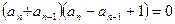 ,
, 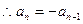 或
或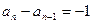 .
.
当 ,
,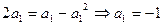 ,若
,若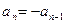 ,则
,则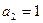 ,这与
,这与 矛盾.
矛盾.
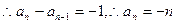 .
.
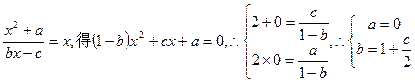
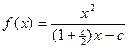 ,
,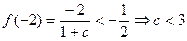 ,
,又
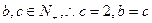
 ,
,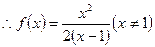
⑵由已知得

两式相减得
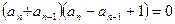 ,
, 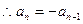 或
或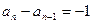 .
.当
 ,
,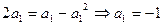 ,若
,若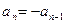 ,则
,则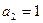 ,这与
,这与 矛盾.
矛盾.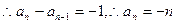 .
.
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
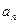 }满足
}满足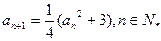 。
。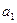 为奇数,则对一切
为奇数,则对一切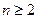 ,
,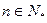 ,都有
,都有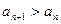 ,求
,求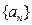 满足性质:对于
满足性质:对于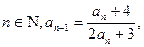 且
且 求
求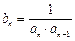 ,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.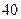 %,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
%,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化. 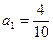 ,经过
,经过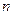 年后绿化的面积为
年后绿化的面积为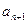 ,试用
,试用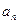 表示
表示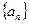 的第
的第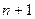 项
项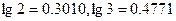 )
)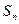 为等差数列
为等差数列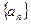 的前
的前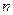 项和,
项和,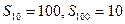 ,求
,求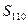 .
.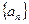 中,
中,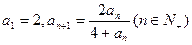 ,求数列
,求数列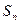 是数列
是数列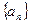 的前
的前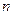 项和,
项和, 则
则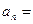 .
.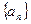 中,
中, 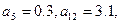 求
求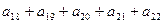 的值
的值