Question

【题目】如图，在四棱锥PABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD＝1，BC＝3，CD＝4，PD＝2.

(1)求异面直线AP与BC所成角的余弦值；

(2)求证：PD⊥平面PBC；

(3)求直线AB与平面PBC所成角的正弦值．

Answer 1

【答案】（1）（2）见解析（3）

【解析】

（Ⅰ）由已知AD∥BC，从而∠DAP或其补角即为异面直线AP与BC所成的角，由此能求出异面直线AP与BC所成角的余弦值．
（Ⅱ）由AD⊥平面PDC，得AD⊥PD，由BC∥AD，得PD⊥BC，再由PD⊥PB，得到PD⊥平面PBC．
（Ⅲ）过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角，由PD⊥平面PBC，得到∠DFP为直线DF和平面PBC所成的角，由此能求出直线AB与平面PBC所成角的正弦值．

(1)如图，由已知AD∥BC，故∠DAP或其补角即为异面直线AP与BC所成的角．

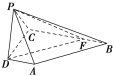
因为AD⊥平面PDC，直线PD平面PDC，所以AD⊥PD.

在Rt△PDA中，由已知，得AP＝，

故cos∠DAP＝＝.

所以，异面直线AP与BC所成角的余弦值为.

(2)证明：由(1)知AD⊥PD.又因为BC∥AD，所以PD⊥BC.又PD⊥PB，PB∩BC＝B，所以PD⊥平面PBC.

(3)解：过点D作DF∥AB，交BC于点F，连接PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角．

因为PD⊥平面PBC，所以PF为DF在平面PBC上的射影，

所以∠DFP为直线DF和平面PBC所成的角．

由于AD∥BC，DF∥AB，故BF＝AD＝1.

由已知，得CF＝BC－BF＝2.

又AD⊥DC，所以BC⊥DC.

在Rt△DCF中，可得DF＝2，

在Rt△DPF中，可得sin∠DFP＝.

所以直线AB与平面PBC所成角的正弦值为.