题目内容
9.已知f(x)=|log2x|,g(x)=f(x)-m,函数y=g(x)有两个零点x1,x2.(1)求 f($\frac{1}{2}$),f(2)的值;
(2)求实数m的取值范围;
(3)求证x1.x2=1.
分析 (1)利用对数运算可得f($\frac{1}{2}$)=|log2$\frac{1}{2}$|=1,f(2)=|log22|=1;
(2)作函数f(x)=|log2x|的图象,从而确定实数m的取值范围;
(3)由题意可得|log2x1|=|log2x2|,即log2x1+log2x2=0,从而证明.
解答 解:(1)f($\frac{1}{2}$)=|log2$\frac{1}{2}$|=1,f(2)=|log22|=1;
(2)作函数f(x)=|log2x|的图象如下,
结合图象可知,实数m的取值范围为(0,+∞);
(3)证明:∵x1,x2是函数y=g(x)的两个零点,
∴|log2x1|=|log2x2|,
即log2x1+log2x2=0,
即log2(x1x2)=0,
故x1.x2=1.
点评 本题考查了对数函数的应用及对数运算的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的首项
的首项 ,前
,前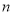 项和为
项和为 ,且
,且 ,则数列
,则数列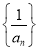 的前5项和为( )
的前5项和为( ) B.
B.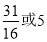 C.
C. D.
D.