题目内容
甲、乙两人用农药治虫,由于计算错误,在A,B两个喷雾器中分别配制成12%和6%的药水各10千克,实际要求两个喷雾器中的农药的浓度是一样的,现在只有两个能容纳1千克药水的药瓶,他们从A,B两个喷雾器中分别取1千克的药水,将A中取得的倒入B中,B中取得的倒入A中,这样操作进行了n次后,A喷雾器中药水的浓度为an%,B喷雾器中药水的浓度为bn%.
(1)证明an+bn是一个常数.
(2)求an与an-1的关系式.
(3)求an的表达式.
(1)证明an+bn是一个常数.
(2)求an与an-1的关系式.
(3)求an的表达式.
(1)见解析 (2) an= an-1+
an-1+ (3) an=3(
(3) an=3( )n+9
)n+9
 an-1+
an-1+ (3) an=3(
(3) an=3( )n+9
)n+9【思路点拨】(1)显然不论如何操作,两种农药中含有的溶质是不变的,这是问题的实际应用.(2)建立第n-1次操作后两种药水的浓度和第n次操作后A喷雾器中药水浓度的关系式.(3)利用(1)(2)的结果求解递推数列.
解:(1)开始时,A中含有10×12%=1.2千克的农药,B中含有10×6%=0.6千克的农药,n次操作后,A中含有10×an%=0.1an千克的农药,B中含有10×bn%=0.1bn千克的农药,它们的和应与开始时农药的质量和相等,从而有0.1an+0.1bn=1.2+0.6,所以an+bn=18(常数).
(2)第n次操作后,A中10千克药水中农药的质量具有关系式:9×an-1+1×bn-1=10an,
由(1)知bn-1=18-an-1,代入化简得an= an-1+
an-1+ .
.
(3)令an+λ= (an-1+λ),利用待定系数法可求出
(an-1+λ),利用待定系数法可求出
λ=-9,
所以an-9= (an-1-9),可知数列{an-9}是以a1-9为首项,
(an-1-9),可知数列{an-9}是以a1-9为首项, 为公比的等比数列,
为公比的等比数列,
由an= an-1+
an-1+ 得,a1=
得,a1= ×12+
×12+ =
=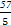 =11.4,
=11.4,
由等比数列的通项公式知:
an-9=(a1-9)( )n-1=2.4(
)n-1=2.4( )n-1=
)n-1= (
( )n-1
)n-1
=3( )n,
)n,
所以an=3( )n+9.
)n+9.
解:(1)开始时,A中含有10×12%=1.2千克的农药,B中含有10×6%=0.6千克的农药,n次操作后,A中含有10×an%=0.1an千克的农药,B中含有10×bn%=0.1bn千克的农药,它们的和应与开始时农药的质量和相等,从而有0.1an+0.1bn=1.2+0.6,所以an+bn=18(常数).
(2)第n次操作后,A中10千克药水中农药的质量具有关系式:9×an-1+1×bn-1=10an,
由(1)知bn-1=18-an-1,代入化简得an=
 an-1+
an-1+ .
.(3)令an+λ=
 (an-1+λ),利用待定系数法可求出
(an-1+λ),利用待定系数法可求出λ=-9,
所以an-9=
 (an-1-9),可知数列{an-9}是以a1-9为首项,
(an-1-9),可知数列{an-9}是以a1-9为首项, 为公比的等比数列,
为公比的等比数列,由an=
 an-1+
an-1+ 得,a1=
得,a1= ×12+
×12+ =
=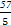 =11.4,
=11.4,由等比数列的通项公式知:
an-9=(a1-9)(
 )n-1=2.4(
)n-1=2.4( )n-1=
)n-1= (
( )n-1
)n-1=3(
 )n,
)n,所以an=3(
 )n+9.
)n+9.
练习册系列答案
相关题目
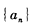 中,
中,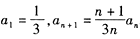
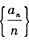 是等比数列,并求
是等比数列,并求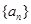 是等差数列,首项
是等差数列,首项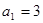 ,前
,前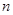 项和为
项和为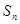 .令
.令 ,
,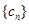 的前
的前 项和
项和 .数列
.数列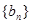 是公比为
是公比为 的等比数列,前
的等比数列,前 ,且
,且 ,
, .
. 的通项公式;
的通项公式;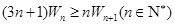 .
.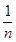 )2an(n∈N*),则数列{an}的通项公式为 .
)2an(n∈N*),则数列{an}的通项公式为 . Sn+1,n∈N*.
Sn+1,n∈N*.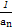 }的前n项和Tn.
}的前n项和Tn.