题目内容

F1、F2是椭圆
x2
9
+
y2
7
=1的两个焦点，A为椭圆上一点，且∠F1AF2=60°，则△F1AF2的面积为（　　）
A．
7
3
3
B．
7
2
C．
7
4
D．
7
5
2
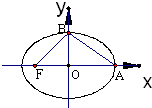
依题意，作图如下：
∵a2=9，b2=7，
∴c2=a2-b2=2，
又|AF1|+|AF2|=2a=6，|F1F2|=2c=2
2
，∠F1AF2=60°，
在△F1AF2中，由余弦定理得：
|F1F2|2=|AF1|2+|AF2|2-2|AF1|•|AF2|cos∠F1AF2
=(|AF1|+|AF2|)2-3|AF1|•|AF2|，
即4c2=4a2-3|AF1|•|AF2|，
∴3|AF1|•|AF2|=4b2=28，
∴|AF1|•|AF2|=
28
3
，
∴△F1AF2的面积S=
1
2
|AF1|•|AF2|sin∠F1AF2=
1
2
×
28
3
×
3
2
=
7
3
3
．
故选：A．
练习册系列答案
相关题目
过椭圆
x2
36
+
y2
25
=1的焦点F1作直线l交椭圆于A、B两点，F2是此椭圆的另一个焦点，则△ABF2的周长为______．
在平面直角坐标系中，已知一个椭圆的中心在原点，左焦点为F(-
3
，0)，且过D（2，0）．
（1）求该椭圆的标准方程；
（2）若P是椭圆上的动点，点A（1，0），求线段PA中点M的轨迹方程．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，其左、右两焦点分别为F1、F2．直线L经过椭圆C的右焦点F2，且与椭圆交于A、B两点．若A、B、F1构成周长为4
2
的△ABF1，椭圆上的点离焦点F2最远距离为
2
+1，且弦AB的长为
4
2
3
，求椭圆和直线L的方程．
设P为椭圆
x2
16
+
y2
9
=1上的一点，F1、F2是椭圆的焦点，若|PF1|：|PF2|=3：1，则∠F1PF2的大小为（　　）
A．30°B．60°C．90°D．120°
如图，椭圆中心在坐标原点，F为左焦点，当
FB
⊥
AB
时，其离心率为
5
-1
2
，此类椭圆被称为“黄金椭圆”，类比“黄金椭圆”，可推算出“黄金双曲线”的离心率为（　　）
A．
5
+1
2
B．
5
-1
2
C．
5
+1		D．
5
-1
已知动点P（x，y）满足：
(x+1)2+y2
+
(x-1)2+y2
=4，则点P的轨迹的离心率是______．
椭圆：
x2
a2
+
y2
b2
=1（a＞b＞0），左右焦点分别是F1，F2，焦距为2c，若直线y=
3
(x+c)与椭圆交于M点，满足∠MF1F2=2∠MF2F1，则离心率是（　　）
A．
2
2
B．
3
-1		C．
3
-1
2
D．
3
2
椭圆的长轴为A1A2，B为短轴一端点，若∠A1BA2=120°，则椭圆的离心率为（　　）
A．
6
3
B．
3
3
C．
3
2
D．
1
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网