题目内容
【题目】已知等差数列{an}的首项为a1 ， 公差为d，其前n项和为Sn ， 若直线y=a1x+m与圆x2+（y﹣1）2=1的两个交点关于直线x+y﹣d=0对称，则数列（ 
）的前100项的和为 ．
【答案】
【解析】解：依题意，直线x+y﹣d=0的斜率为﹣1， 则a1=1，
又∵直线y=a1x+m与圆x2+（y﹣1）2=1的两个交点关于直线x+y﹣d=0对称，
∴直线x+y﹣d=0必过圆心，
即0+1﹣d=0，d=1，
∴数列{an}是首项、公差均为1的等差数列，
∴Sn=n+ 
= 
，
∴ 
，
∴数列{ 
}的前100项的和为 
，
所以答案是： ．
【考点精析】根据题目的已知条件，利用数列的前n项和的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系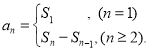
．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
