题目内容
21.在XOY平面上有一点列P1(a1,b1),P2(a2,b2)…Pn(an,bn),…,对每个自然数n,点Pn位于函数y=2000((1)求点Pn的纵坐标bn的表达式;
(2)若对每个自然数n,以bn,bn-1,bn-2为边长能构成一个三角形,求a的取值范围;
(3)设Bn=b1b2…bn(n![]() N).若a取(2)中确定的范围内的最小整数,求数列
N).若a取(2)中确定的范围内的最小整数,求数列![]() 的最大项的项数.
的最大项的项数.
21.解:
(1)由题意,an=n+![]() ,
,
∴bn=![]() .
.
(2)∵函数y=![]() (0<a<10)递减,
(0<a<10)递减,
∴对每个自然数n,有bn>bn+1>bn+2.
则以bn,bn+1,bn+2为边长能构成一个三角形的充要条件是bn+2+bn+1>bn,
即![]() -1>0.
-1>0.
解得a<-5(1+![]() )或a>5(
)或a>5(![]() ),
),
∴5(![]() -1)<a<10.
-1)<a<10.
(3)∵5(![]() -1)<a<10,
-1)<a<10,
∴a=7,bn=![]() .
.
数列{bn}是一个递减的正数数列,对每个自然数n≥2,Bn=bnBn-1.
于是当bn≥1时,Bn≥Bn-1,当bn<1时,Bn<Bn-1.
因此,数列{Bn}的最大项的项数n满足不等式bn≥1且bn-1<1.
由bn=![]() ≥1,得n≤20.8.
≥1,得n≤20.8.
∴n=20.

练习册系列答案
相关题目
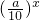 (0<a<10)的图象上,且点Pn(an,bn)与点(n,0)和(n+1,0)构成一个以点Pn(an,bn)为顶点的等腰三角形.
(0<a<10)的图象上,且点Pn(an,bn)与点(n,0)和(n+1,0)构成一个以点Pn(an,bn)为顶点的等腰三角形.