题目内容
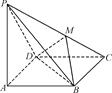
在空间四边形ABCD中,已知AC⊥BD,AD⊥BC,求证:AB⊥CD.
见解析
过A点作AO垂直平面BCD于O,连结BO,CO,DO.
∵AO⊥平面BCD,∴AO⊥BD.
又AC⊥BD,∴BD⊥平面AOC,∴CO⊥BD.
同理,DO⊥BC,∴O为△BCD的垂心,∴BO⊥CD.
又AO⊥平面BCD,∴AO⊥CD,
∴CD⊥平面ABO,∴AB⊥CD.
∵AO⊥平面BCD,∴AO⊥BD.
又AC⊥BD,∴BD⊥平面AOC,∴CO⊥BD.
同理,DO⊥BC,∴O为△BCD的垂心,∴BO⊥CD.
又AO⊥平面BCD,∴AO⊥CD,
∴CD⊥平面ABO,∴AB⊥CD.

练习册系列答案
相关题目
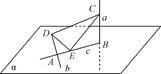
 ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
 ;若不存在,说明理由.
;若不存在,说明理由.
 AC,D、E、F分别为线段AC、A1A、C1B的中点.
AC,D、E、F分别为线段AC、A1A、C1B的中点.
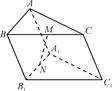
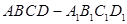 中,线段
中,线段 上(不包括端点)各有一点
上(不包括端点)各有一点 ,且
,且 ,下列说法中,不正确的是( )
,下列说法中,不正确的是( ) 四点共面
四点共面 与平面
与平面 所成的角为定值
所成的角为定值
 的大小为
的大小为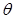 ,则
,则 的最小值为
的最小值为