题目内容
17．在△ABC中，若（2a-c）tanC=ctanB，求B．分析 由条件利用同角三角函数的基本关系、正弦定理、两角和的正弦公式求得2sinAcosB=sin（B+C），由此求得cosB的值，可得B的值．
解答 解：△ABC中，若（2a-c）tanC=ctanB，
则$\frac{tanB}{tanC}$=$\frac{2a-c}{c}$，即 $\frac{sinBcosC}{cosBsinC}$=$\frac{2sinA-sinC}{sinC}$．
化简可得2sinAcosB=sin（B+C），
求得cosB=$\frac{1}{2}$，
∴B=60°．
点评 本题主要考查同角三角函数的基本关系、诱导公式、两角和的正弦公式以及正弦定理的应用，属于基础题．
练习册系列答案
相关题目
已知直二面角α-l-β，点A∈α，AC⊥l，C为垂足，点B∈α，BD⊥l，D为垂足，若AB=2，AC=BD=1，求D到平面ABC的距离．
6．
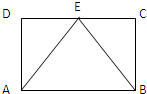如图，矩形ABCD中，点E为边CD的中点，若在矩形ABCD内部随机抽取一个点Q，则点Q取自△ABE内部的概率等于（ ）
如图，矩形ABCD中，点E为边CD的中点，若在矩形ABCD内部随机抽取一个点Q，则点Q取自△ABE内部的概率等于（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |