题目内容
对于函数f(x)=-| 1 |
| 4 |
| 2 |
| 3 |
(1)求实数a的值;
(2)若关于x的方程f(3x)=m有三个不等实根,求实数m的取值范围.
分析:(1)求出导函数,令x=1求出f′(1)的值,再将(1,-2)代入f(x)求出m的值;求出g′(x)令其x=1求出g′(1)=0求出a值;求出g′(x)=0的根,判断出根左右两边的符号,求出极小值.
(2)先得出f(x)=-
x4+
x3+
x2-2x-2.再利用导数研究其单调性及极值,从而得出函数y=f(x)的大致图象,令3x=t(t>0),若关于x的方程f(3x)=m有三个不等实根,则关于t的方程f(t)=m在(0,+∞)上有三个不等实根,即函数y=f(t)的图象与直线y=m在(0,+∞)上有三个不同的交点.最后由图象可知m的取值范围.
(2)先得出f(x)=-
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
解答: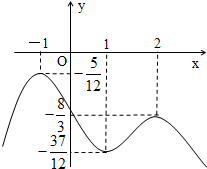 解:(1)f′(x)=-x3+2x2+2ax-2. (1分)
解:(1)f′(x)=-x3+2x2+2ax-2. (1分)
据题意,当x=-1时f(x)取极值,所以f′(-1)=0. (2分)
因为f′(-1)=-(-1)3+2×(-1)2+2a×(-1)-2=1-2a.
由1-2a=0,得a=
. (4分)
(2)因为a=
,则f(x)=-
x4+
x3+
x2-2x-2.
所以f′(x)=-x3+2x2+x-2=-(x-1)(x+1)(x-2).
由f′(x)>0,得(x-1)(x+1)(x-2)<0,即x<-1或1<x<2.
所以f(x)在区间(-∞,-1),(1,2)上单调递增,
在区间(-1,1),(2,+∞)上单调递减.(6分)
所以f(x)的极大值为f(-1)=-
,f(2)=-
,
极小值为f(1)=-
. (7分)
由此可得函数y=f(x)的大致图象如下:(8分)
令3x=t(t>0),若关于x的方程f(3x)=m有三个不等实根,
则关于t的方程f(t)=m在(0,+∞)上有三个不等实根,
即函数y=f(t)的图象与直线y=m在(0,+∞)上有三个不同的交点.
又f(0)=-2>-
,由图象可知,-
<m<-
,
故m的取值范围是(-
,-
). (9分)
 解:(1)f′(x)=-x3+2x2+2ax-2. (1分)
解:(1)f′(x)=-x3+2x2+2ax-2. (1分)据题意,当x=-1时f(x)取极值,所以f′(-1)=0. (2分)
因为f′(-1)=-(-1)3+2×(-1)2+2a×(-1)-2=1-2a.
由1-2a=0,得a=
| 1 |
| 2 |
(2)因为a=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
所以f′(x)=-x3+2x2+x-2=-(x-1)(x+1)(x-2).
由f′(x)>0,得(x-1)(x+1)(x-2)<0,即x<-1或1<x<2.
所以f(x)在区间(-∞,-1),(1,2)上单调递增,
在区间(-1,1),(2,+∞)上单调递减.(6分)
所以f(x)的极大值为f(-1)=-
| 5 |
| 12 |
| 8 |
| 3 |
极小值为f(1)=-
| 37 |
| 12 |
由此可得函数y=f(x)的大致图象如下:(8分)
令3x=t(t>0),若关于x的方程f(3x)=m有三个不等实根,
则关于t的方程f(t)=m在(0,+∞)上有三个不等实根,
即函数y=f(t)的图象与直线y=m在(0,+∞)上有三个不同的交点.
又f(0)=-2>-
| 8 |
| 3 |
| 37 |
| 12 |
| 8 |
| 3 |
故m的取值范围是(-
| 37 |
| 12 |
| 8 |
| 3 |
点评:本题考查曲线的切线问题时,常利用的是切线的导数在切点处的导数值为切线的斜率;解决函数的极值问题唯一的方法是利用导数.

练习册系列答案
相关题目