题目内容
若x、y满足(x-1)2+(y+2)2=4,求S=2x+y的最大值和最小值.
S的最大值是2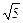 ,最小值为-2
,最小值为-2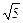 .
.
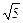 ,最小值为-2
,最小值为-2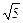 .
.由(x-1)2+(y+2)2=22可知,它表示以(1,-2)为圆心,半径等于2的圆.
令x=1+2cosθ,y=-2+2sinθ,
则S=2x+y=2+4cosθ-2+2sinθ=4cosθ+2sinθ.
∴|S|≤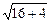 =2
=2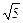 ,
,
即-2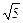 ≤S≤2
≤S≤2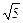 .
.
∴S的最大值是2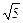 ,最小值为-2
,最小值为-2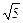 .
.
令x=1+2cosθ,y=-2+2sinθ,
则S=2x+y=2+4cosθ-2+2sinθ=4cosθ+2sinθ.
∴|S|≤
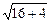 =2
=2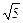 ,
,即-2
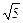 ≤S≤2
≤S≤2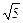 .
.∴S的最大值是2
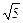 ,最小值为-2
,最小值为-2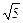 .
.
练习册系列答案
相关题目
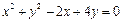 按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使
按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使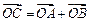 =λa,求直线l的方程及对应的点C的坐标.
=λa,求直线l的方程及对应的点C的坐标.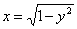 有且仅有一个公共点,则b的取值范围是( )
有且仅有一个公共点,则b的取值范围是( ) 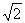
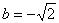
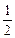 ]
]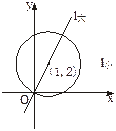
 上任意一点P( ),不等式
上任意一点P( ),不等式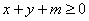 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 与直线
与直线 有两个交点时,实数
有两个交点时,实数 的取值范围是
的取值范围是 


