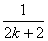题目内容
(本小题12分)试用含 的表达式表示
的表达式表示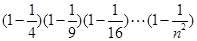 的值,并用数学归纳法证明你的结论.
的值,并用数学归纳法证明你的结论.
 的表达式表示
的表达式表示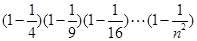 的值,并用数学归纳法证明你的结论.
的值,并用数学归纳法证明你的结论.解:猜想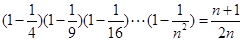 …………………………..4分
…………………………..4分
证明: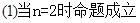
(2)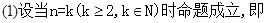
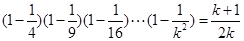
则当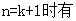
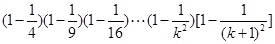
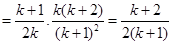
所以,命题在n=k+1时也成立,综合(1),(2),命题对任何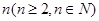 都成立。
都成立。
……………………………………12分
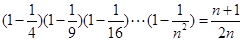 …………………………..4分
…………………………..4分证明:
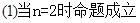
(2)
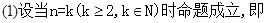
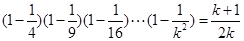
则当
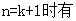
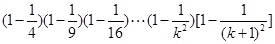
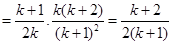
所以,命题在n=k+1时也成立,综合(1),(2),命题对任何
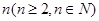 都成立。
都成立。……………………………………12分
略

练习册系列答案
相关题目
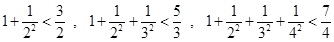 , … … ,
, … … ,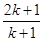
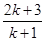
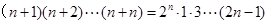 (
(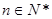 )时,从“
)时,从“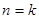 到
到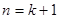 ”左边需增乘的代数式为( )
”左边需增乘的代数式为( )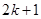
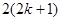
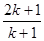
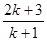
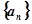 的前
的前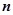 项和为
项和为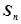 ,满足
,满足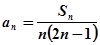 ,且
,且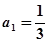 .
.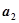 ,
,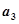 ,
,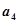 ;
; 对于一切
对于一切 都成立?
都成立?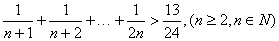 ”的过程中,
”的过程中,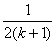
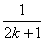 和
和