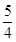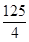题目内容
为了了解青少年视力情况,某市从高考体检中随机抽取16名学生的视力进行调查,经医生用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
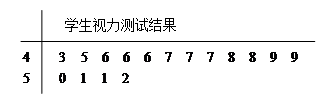
(1)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(2)以这16人的样本数据来估计该市所有参加高考学生的的总体数据,若从该市参加高考的学生中任选3人,记 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.
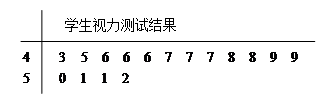
(1)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(2)以这16人的样本数据来估计该市所有参加高考学生的的总体数据,若从该市参加高考的学生中任选3人,记
 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.(1)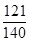 ;(2)分布列为
;(2)分布列为
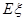
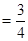 .
.
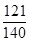 ;(2)分布列为
;(2)分布列为 |  | 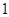 | 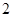 | 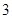 |
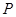 | 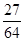 | 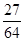 | 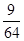 |  |
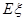
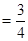 .
. 试题分析:(1)注意事件“至多有1人是“好视力”的”等于事件“恰有0人是“好视力”的”与“恰有有1人是“好视力”的”的和,而这两个事件是互斥事件,先算出这两个事件的概率,由互斥事件的概率和公式就可求得所求的概率;(2)首先写出
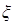 的所有可能取值为0、1、2、3,既然是以以这16人的样本数据来估计该市所有参加高考学生的的总体数据,则从该市参加高考的学生中任选1人是“好视力”学生的概率为
的所有可能取值为0、1、2、3,既然是以以这16人的样本数据来估计该市所有参加高考学生的的总体数据,则从该市参加高考的学生中任选1人是“好视力”学生的概率为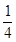 ,不是“好视力”学生的概率为
,不是“好视力”学生的概率为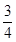 ,抽3人就是将“每次抽1人”的试验重复做三次,所以
,抽3人就是将“每次抽1人”的试验重复做三次,所以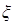 服从参数为3和
服从参数为3和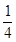 的二项分布,由n次独立重复试验恰有k次发生的概率公式
的二项分布,由n次独立重复试验恰有k次发生的概率公式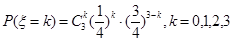 可求得
可求得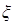 的分布列,进而可求得其数学期望.
的分布列,进而可求得其数学期望.试题解析:(1)设
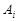 表示所取3人中有
表示所取3人中有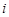 个人是“好视力”,至多有1人是“好视力”记为事件
个人是“好视力”,至多有1人是“好视力”记为事件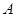 ,
,则
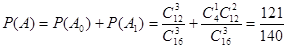 6分
6分(2)
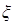 的可能取值为0、1、2、3 7分
的可能取值为0、1、2、3 7分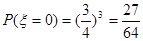 ;
; 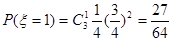
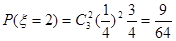 ;
;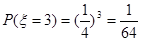
分布列为
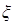 |  | 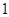 | 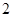 | 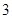 |
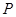 | 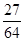 | 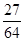 | 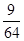 | 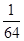 |
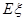
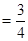 . 12分
. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
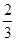 和
和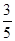 ,现安排甲组研发新产品
,现安排甲组研发新产品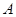 ,乙组研发新产品
,乙组研发新产品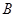 .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.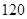 万元,若新产品
万元,若新产品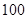 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
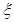 服从二项分布
服从二项分布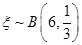 ,则
,则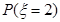 的值为 .
的值为 .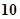 环、
环、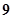 环、
环、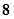 环的概率分别是
环的概率分别是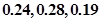 ,则这位射手在一次射击中不够
,则这位射手在一次射击中不够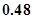
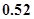
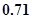
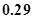
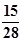
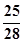
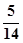
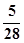
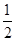
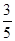
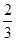
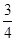
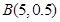 ,又η=5ξ,则Eη和Dη的值分别是( )
,又η=5ξ,则Eη和Dη的值分别是( )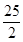 和
和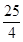
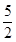 和
和