题目内容
某射手一次射击中,击中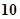 环、
环、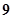 环、
环、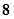 环的概率分别是
环的概率分别是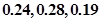 ,则这位射手在一次射击中不够
,则这位射手在一次射击中不够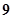 环的概率是( )
环的概率是( )
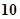 环、
环、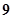 环、
环、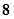 环的概率分别是
环的概率分别是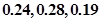 ,则这位射手在一次射击中不够
,则这位射手在一次射击中不够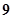 环的概率是( )
环的概率是( )A.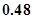 | B.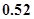 | C.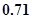 | D.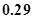 |
A
试题分析:由已知某射手一次射击中,击中
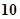 环、
环、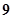 环、
环、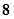 环的事件是互斥的,而事件:“这位射手在一次射击中不够
环的事件是互斥的,而事件:“这位射手在一次射击中不够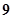 环”的对立事件为:“这位射手在一次射击中
环”的对立事件为:“这位射手在一次射击中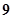 环或10环”,故所求概率P=1-(0.28+0.24)=0.48.故选A.
环或10环”,故所求概率P=1-(0.28+0.24)=0.48.故选A.
练习册系列答案
相关题目
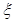 .
.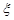 的数学期望和方差.
的数学期望和方差.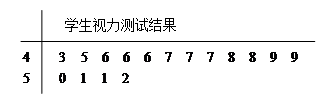
 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求
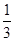 .
.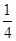 ,不堵车的概率为
,不堵车的概率为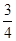 ;校车走公路②堵车的概率为
;校车走公路②堵车的概率为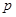 ,不堵车的概率为
,不堵车的概率为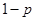 .若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响. ,求走公路②堵车的概率;
,求走公路②堵车的概率;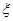 的分布列和数学期望.
的分布列和数学期望.