题目内容
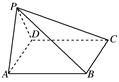
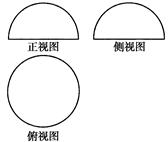
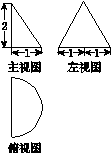
一个几何体的三视图如图所示,其中主视图和左视图是腰长为4的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )
| A．12π | B．24π |
| C．32π | D．48π |
D
由几何体的三视图可知,其直观图如图所示,
将其补成一个正方体可发现该四棱锥外接球球心为SB的中点,球半径R=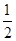
SB=
=2
,
∴S球=4π·(2)2=48π.
将其补成一个正方体可发现该四棱锥外接球球心为SB的中点,球半径R=
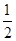SB==2,∴S球=4π·(2
)2=48π.
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
=2”.若把该结论推广到空间,则有结论:“在六条棱长都相等的四面体ABCD中,若M是△BCD的三边中线的交点,O为四面体ABCD外接球的球心,则
= .”
