题目内容
已知结论:“在三边长都相等的△ABC中,若D是BC的中点,G是△ABC外接圆的圆心,则 =2”.若把该结论推广到空间,则有结论:“在六条棱长都相等的四面体ABCD中,若M是△BCD的三边中线的交点,O为四面体ABCD外接球的球心,则
=2”.若把该结论推广到空间,则有结论:“在六条棱长都相等的四面体ABCD中,若M是△BCD的三边中线的交点,O为四面体ABCD外接球的球心,则 = .”
= .”
 =2”.若把该结论推广到空间,则有结论:“在六条棱长都相等的四面体ABCD中,若M是△BCD的三边中线的交点,O为四面体ABCD外接球的球心,则
=2”.若把该结论推广到空间,则有结论:“在六条棱长都相等的四面体ABCD中,若M是△BCD的三边中线的交点,O为四面体ABCD外接球的球心,则 = .”
= .”3
如图所示,易知球心O在线段AM上,
不妨设四面体ABCD的棱长为1,外接球的半径为R,

则BM= ×
× =
= ,
,
AM= =
= ,
,
R= ,
,
解得R= .
.
于是, =
=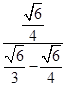 =3.
=3.
不妨设四面体ABCD的棱长为1,外接球的半径为R,

则BM=
 ×
× =
= ,
,AM=
 =
= ,
,R=
 ,
,解得R=
 .
.于是,
 =
=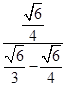 =3.
=3.
练习册系列答案
相关题目







 π+12
π+12 A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号).
A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号). 
 时,S为四边形;
时,S为四边形; 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R= ;
; .
. a的正三角形,则原△ABC的面积为( )
a的正三角形,则原△ABC的面积为( ) a2
a2 a2
a2 a2
a2


 )
)
