题目内容
下列两个函数为相等函数的是( )
A.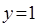 与 与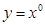 |
B.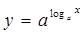 与 与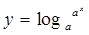 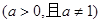 |
C.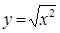 与 与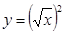 |
D.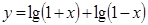 与 与 |
D
解析试题分析:构成函数的要素有两个,一是对应法则,二是定义域。
考察A、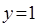 与
与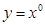 ,前者定义域为R,后者定义域为{x|x
,前者定义域为R,后者定义域为{x|x  0},定义域不同,错;
0},定义域不同,错;
考察B、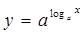 与
与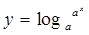
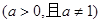 ,前者定义域为(0,+
,前者定义域为(0,+ ),后者定义域为R,定义域不同,错;
),后者定义域为R,定义域不同,错;
考察C、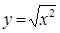 与
与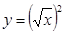 ,前者定义域为R,后者定义域为(0,+
,前者定义域为R,后者定义域为(0,+ ),定义域不同,错。故选D。
),定义域不同,错。故选D。
考点:本题主要考查函数的概念,指数函数、对数函数的性质。
点评:简单题,构成函数的要素有两个,一是对应法则,二是定义域。

练习册系列答案
相关题目
函数 的定义域为
的定义域为
A.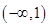 | B.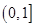 | C.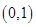 | D.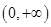 |
若定义在R上的偶函数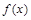 对任意
对任意
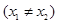 ,有
,有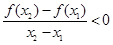 ,则
,则
A.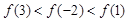 | B.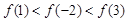 |
C.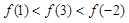 | D. |
对于定义域为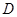 的函数
的函数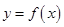 和常数
和常数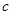 ,若对任意正实数
,若对任意正实数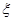 ,
,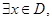 使得
使得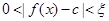 恒成立,则称函数
恒成立,则称函数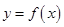 为“敛
为“敛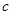 函数”.现给出如下函数:
函数”.现给出如下函数:
①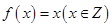 ; ②
; ②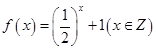 ;
;
③ 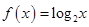 ; ④
; ④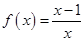 .
.
其中为“敛1函数”的有
| A.①② | B.③④ | C.②③④ | D.①②③ |
设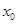 是函数
是函数 的零点,若有
的零点,若有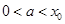 ,则
,则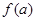 的值满足
的值满足
A.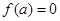 | B. | C. | D.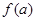 的符号不确定 的符号不确定 |
函数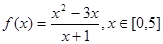 的值域是( )
的值域是( )
| A.[0,2] | B.[0,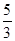 ] ] | C.[-1,2] | D.[-1,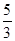 ] ] |
 则
则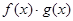 的图象为( )
的图象为( )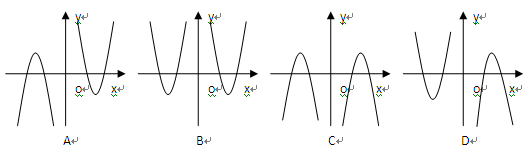


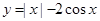 的图象大致是
的图象大致是 