题目内容
20．函数y=1+sinx，（x∈[-π，π]）的图象与直线y=$\frac{3}{2}$的交点的个数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 根据曲线与方程之间的关系，直接解方程即可得到结论．
解答 解：由y=1+sinx=$\frac{3}{2}$得sinx=$\frac{1}{2}$，
∴当x∈[-π，π]时，x=$\frac{π}{6}$或x=$\frac{5π}{6}$，
即方程有2个解，即两条曲线的图象的交点个数为2个．
故选：C．
点评 本题主要考查函数交点个数的判断，利用函数和方程之间的关系，直接进行求解即可，比较基础．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
15．函数f（x）=logax的图象如图所示，则a的取值可能是（ ）
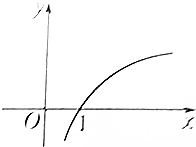
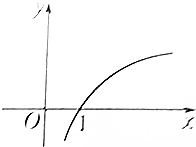
| A． | 10 | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
15．如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（x吨）与相应的生产能耗y（吨）标准煤的几组对照数据：
（1）请根据上表提供的前四列数据，用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=bx+a；
（2）在误差不超过0.05的条件下，利用X=7，X=8来检验（1）所求回归直线是否合适？
（3）已知该厂技术改造前100吨甲产品能耗为90吨标准煤，试根据（1）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（参考：用最小二乘法求线性回归方程系数公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$）
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 2.5 | 3 | 4 | 4.5 | 5.22 | 5.97 |
（2）在误差不超过0.05的条件下，利用X=7，X=8来检验（1）所求回归直线是否合适？
（3）已知该厂技术改造前100吨甲产品能耗为90吨标准煤，试根据（1）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（参考：用最小二乘法求线性回归方程系数公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$）