题目内容
【题目】已知锐角△ABC中，内角
所对应的边分别为
，且满足：
，
，则
的取值范围是____________．
【答案】
【解析】分析：由已知可得：b2=2a+a2，又由余弦定理可得：b2=a2+4-4acosB，整理可得：
，可求B的范围，进而可求cosB的范围，进而可求a的范围．
详解：：∵b2-a2=ac，c=2，可得：b2=2a+a2，又∵由余弦定理可得：b2=a2+c2-2accosB=a2+4-4acosB，
∴2a+a2=a2+4-4acosB，整理可得：，∵由余弦定理2bccosA=b2+c2-a2=c2+ac，可得：2bcosA=c+a，
∴由正弦定理可得：2sinBcosA=sinC+sinA=sin（A+B）+sinA=sinAcosB+cosAsinB+sinA，
可得：sinBcosA-sinAcosB=sinA，可得：sin（B-A）=sinA，可得：B-A=A，或B-A=π-A（舍去），可得：B=2A，C=π-A-B=π-3A，由△ABC为锐角三角形，可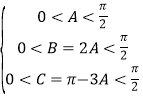得：
解得：
可得：cosB∈
,∴可得：1+2cosB∈（1，2），∈（1，2），故答案为：（1，2）．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
