题目内容
15．已知函数f（x）=|x-2|，g（x）=-|x+3|+m．（1）解关于x的不等式f（x）-$\frac{1}{4}$x-1＞0；
（2）若函数f（x）的图象恒在函数g（x）图象的上方，求m的取值范围．
分析 （1）关于x的不等式f（x）-$\frac{1}{4}$x-1＞0，即|x-2|＞$\frac{x}{4}$+1，即x-2＞$\frac{x}{4}$+1 或x-2＜-（ $\frac{x}{4}$+1 ），由此求得它的解集．
（2）若函数f（x）的图象恒在函数g（x）图象的上方，画出图形，数形结合求得m的范围．
解答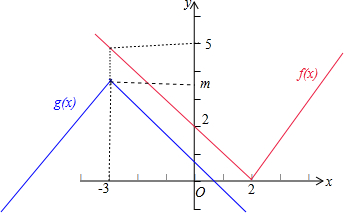 
解：（1）关于x的不等式f（x）-$\frac{1}{4}$x-1＞0，即|x-2|＞$\frac{x}{4}$+1，
∴x-2＞$\frac{x}{4}$+1 或x-2＜-（ $\frac{x}{4}$+1 ）．
求得 x＞4或 x＜$\frac{4}{5}$，故不等式的解集为{x|x＞4或 x＜$\frac{4}{5}$ }．
（2）若函数f（x）的图象恒在函数g（x）图象的上方，如图所示：
故有m＜5．
点评 本题主要考查绝对值不等式的解法，函数的恒成立问题，体现了数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
6．为了得到函数$y=sin2x-\sqrt{3}cos2x$的图象，可以将函数y=4sinxcosx的图象（ ）
| A． | 向右平移$\frac{π}{12}$个单位 | B． | 向左平移$\frac{π}{12}$个单位 | ||
| C． | 向右平移$\frac{π}{6}$个单位 | D． | 向左平移$\frac{π}{6}$个单位 |
某校从参加2015年高考的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六组[90，100），[100，110），…，[140，150]后得到部分频率分布直方图（如图所示）．观察图中数据，回答下列问题．
10．若cosα=$\frac{4}{5}$，则cos2α=（ ）
| A． | $\frac{7}{25}$ | B． | -$\frac{7}{25}$ | C． | $\frac{3}{5}$ | D． | -$\frac{3}{5}$ |
20．已知a＜0，-1＜b＜0，则a，ab，ab2的大小关系式（ ）
| A． | a＞ab＞ab2 | B． | ab2＞ab＞a | C． | ab＞a＞ab2 | D． | ab＞ab2＞a |
7．不论m为何值，直线l：mx+y-2+m=0恒过定点，则定点坐标为（ ）
| A． | （-1，0） | B． | （-1，-2） | C． | （-1，2） | D． | （1，-2） |
4．已知圆的参数方程为$\left\{\begin{array}{l}x=2+\sqrt{2}cosθ\\ y=1+\sqrt{2}sinθ\end{array}\right.（θ为参数）$，那么该圆的普通方程是（ ）
| A． | ${（x-2）^2}+{（y-1）^2}=\sqrt{2}$ | B． | ${（x+2）^2}+{（y+1）^2}=\sqrt{2}$ | C． | （x-2）2+（y-1）2=2 | D． | （x+2）2+（y+1）2=2 |