题目内容
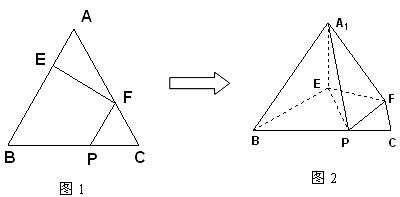
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到![]() 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(III)求二面角B-A1P-F的大小(用反三角函数表示)
解:不妨设正三角形ABC 的边长为 3 .
(I)在图1中,取BE的中点D,连结DF.
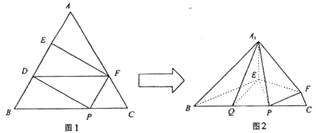
∵AE![]() EB=CF
EB=CF![]() FA=1
FA=1![]() 2,∴AF=AD=2,而∠A=600,
2,∴AF=AD=2,而∠A=600,
∴△ADF是正三角形,又AE=DE=1,∴EF⊥AD
在图2中,A1E⊥EF,BE⊥EF,
∴∠A1EB为二面角A1-EF-B的平面角
由题设条件知此二面角为直二面角,∴A1E⊥BE.
又BE∩EF=E,∴A1E⊥平面BEF,即A1E⊥平面BEP
(II)在图2中,∵A1E不垂直于A1B,∴A1E是平面A1BP的斜线.
又A1E⊥平面BEP, ∴A1E⊥BP,
从而BP垂直于A1E在平面A1BP内的射影(三垂线定理的逆定理).
设A1E在平面A1BP内的射影为A1Q,且A1Q交BP于点Q,则
∠EA1Q就是A1E与平面A1BP所成的角,且BP⊥A1Q.
在△EBP中,∵BE=BP=2,∠EBP=600, ∴△EBP是等边三角形,∴BE=EP.
又A1E⊥平面BEP,∴A1B=A1P,∴Q为BP的中点,且EQ=![]()
又A1E=1,在Rt△A1EQ ,tan∠EA1Q=![]() ,∴∠EA1Q=600.
,∴∠EA1Q=600.
所以直线A1E与平面A1BP所成的角为600
(III)在图3中,过F作FM⊥A1P于M,连结QM,QF.
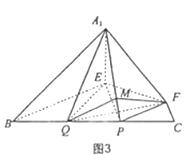
∵CF=CP=1, ∠C=600. ∴△FCP是正三角形,∴PF=1.
又PQ=![]() BP=1,∴PF=PQ. ①
BP=1,∴PF=PQ. ①
∵A1E⊥平面BEP,EQ=EF=![]() , ∴A1F=A1Q,∴△A1FP≌△A1QP,
, ∴A1F=A1Q,∴△A1FP≌△A1QP,
从而∠A1PF=∠A1PQ. ②
由①②及MP为公共边知 △FMP≌△QMP,
∴∠QMP=∠FMP=900,且MF=MQ,
从而∠FMQ为二面角B-A1P-F的平面角
在Rt△A1QP中,A1Q=A1F=2,PQ=1,∴A1P=![]() .
.
∵MQ⊥A1P, ∴MQ=![]() ,∴MF=
,∴MF=![]() .
.
在△FCQ中,FC=1,QC=2,∠C=600,由余弦定理得QF=![]() .
.
在△FMQ中,cos∠FMQ=![]()
所以二面角B-A1P-F的大小为![]() -arccos
-arccos![]()

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案 在正三角形ABC中,E、F分别是AB、AC边上的点,满足
在正三角形ABC中,E、F分别是AB、AC边上的点,满足 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( )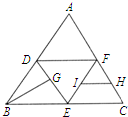 如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将
如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将