题目内容
【题目】已知函数![]()
(1)若函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,求实数
上单调递增,求实数![]() 的值;
的值;
(2)是否存在实数![]() ,使得
,使得![]() 在
在![]() 上单调递减,若存在,试求
上单调递减,若存在,试求![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(3)若![]() ,当
,当![]() 时不等式
时不等式![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)求导函数,根据函数f(x)在(-![]() ,1)上单调递减,在(1,+∞)上单调递增,可得x=1是方程f′(x)=0的根,从而可求实数a的值;(2)由题意得:f′(x)=3x2+2ax-2≤0在(-2,
,1)上单调递减,在(1,+∞)上单调递增,可得x=1是方程f′(x)=0的根,从而可求实数a的值;(2)由题意得:f′(x)=3x2+2ax-2≤0在(-2, ![]() )上恒成立,由此可实数a的取值范围;(3)求导函数,求导函数x∈(-1,2)时,f(x)的最小值,欲使不等式f(x)<m有解,只需m≥[f(x)]min,从而可求实数m的取值范围.
)上恒成立,由此可实数a的取值范围;(3)求导函数,求导函数x∈(-1,2)时,f(x)的最小值,欲使不等式f(x)<m有解,只需m≥[f(x)]min,从而可求实数m的取值范围.
试题解析:
(1)![]() ,
,
∵![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 是方程
是方程![]() 的根,解得
的根,解得![]()
(2)由题意得: ![]() 在
在![]() 上恒成立,
上恒成立,
∴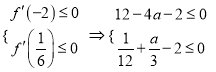 ∴
∴![]()
(3)当![]() 时,
时, ![]() ,
,
由![]() 得:
得: ![]()
列表:
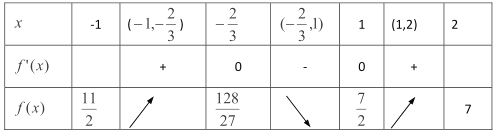
∴![]() 时,
时, ![]() 的最小值为
的最小值为![]() ,此时
,此时![]() ,
,
欲使![]() 有解,只需
有解,只需![]() ,∴
,∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目