题目内容
已知函数f(x)=sin(ωx- )+
)+ cos(ωx-
cos(ωx- )(ω>0),其图象与x轴的一个交点到其邻近一条对称轴的距为
)(ω>0),其图象与x轴的一个交点到其邻近一条对称轴的距为
(1)求f( )的值;
)的值;
(2)将函数f(x)的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到时原来的4倍,纵坐标不变,得到y=g(x)的图象,求[
个单位后,再将得到的图象上各点的横坐标伸长到时原来的4倍,纵坐标不变,得到y=g(x)的图象,求[ ,2π]上的最大值和最小值.
,2π]上的最大值和最小值.
解:(1)由题意函数f(x)=sin(ωx- )+
)+ cos(ωx-
cos(ωx- )(ω>0),
)(ω>0),
其图象与x轴的一个交点到其邻近一条对称轴的距为 ;
;
所以 ,可得T=π,∴ω=
,可得T=π,∴ω=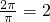 ∴f(x)=sin(2x-
∴f(x)=sin(2x- )+
)+ cos(2x-
cos(2x- )=2sin2x
)=2sin2x
所以f( )=2sin
)=2sin =1
=1
(2)将函数f(x)的图象向右平移 个单位后,得到y=2sin2(x-
个单位后,得到y=2sin2(x- )=2sin(2x-
)=2sin(2x- );
);
再将得到的图象上各点的横坐标伸长到时原来的4倍,得到y=2sin(2× x-
x- )=2sin
)=2sin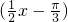 ;
;
∴g(x)=2sin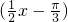 ,
,
∵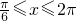 ,∴
,∴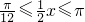
∴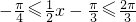
∴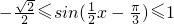
∴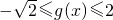
∴当x= 时,g(x)的最小值为:
时,g(x)的最小值为: ;当x=
;当x= 时g(x)的最大值为2.
时g(x)的最大值为2.
分析:(1)图象与x轴的一个交点到其邻近一条对称轴的距为 ,推出函数的周期,利用函数的周期求出ω,化简函数的表达式求出函数的解析式,然后求f(
,推出函数的周期,利用函数的周期求出ω,化简函数的表达式求出函数的解析式,然后求f( )的值;
)的值;
(2)将函数f(x)的图象向右平移 个单位,得到函数的解析式,再将得到的图象上各点的横坐标伸长到时原来的4倍,纵坐标不变,得到y=g(x)的解析式,分析[
个单位,得到函数的解析式,再将得到的图象上各点的横坐标伸长到时原来的4倍,纵坐标不变,得到y=g(x)的解析式,分析[ ,2π]上,推出
,2π]上,推出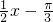 的范围,然后求出函数的最大值和最小值.
的范围,然后求出函数的最大值和最小值.
点评:本题是中档题,考查三角函数的解析式的求法,周期的应用,三角函数的最值的求法,函数的平移变换,考查计算能力.
 )+
)+ cos(ωx-
cos(ωx- )(ω>0),
)(ω>0),其图象与x轴的一个交点到其邻近一条对称轴的距为
 ;
;所以
 ,可得T=π,∴ω=
,可得T=π,∴ω=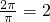 ∴f(x)=sin(2x-
∴f(x)=sin(2x- )+
)+ cos(2x-
cos(2x- )=2sin2x
)=2sin2x 所以f(
 )=2sin
)=2sin =1
=1 (2)将函数f(x)的图象向右平移
 个单位后,得到y=2sin2(x-
个单位后,得到y=2sin2(x- )=2sin(2x-
)=2sin(2x- );
);再将得到的图象上各点的横坐标伸长到时原来的4倍,得到y=2sin(2×
 x-
x- )=2sin
)=2sin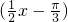 ;
;∴g(x)=2sin
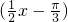 ,
,∵
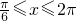 ,∴
,∴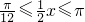
∴
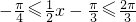
∴
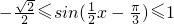
∴
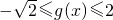
∴当x=
 时,g(x)的最小值为:
时,g(x)的最小值为: ;当x=
;当x= 时g(x)的最大值为2.
时g(x)的最大值为2.分析:(1)图象与x轴的一个交点到其邻近一条对称轴的距为
 ,推出函数的周期,利用函数的周期求出ω,化简函数的表达式求出函数的解析式,然后求f(
,推出函数的周期,利用函数的周期求出ω,化简函数的表达式求出函数的解析式,然后求f( )的值;
)的值;(2)将函数f(x)的图象向右平移
 个单位,得到函数的解析式,再将得到的图象上各点的横坐标伸长到时原来的4倍,纵坐标不变,得到y=g(x)的解析式,分析[
个单位,得到函数的解析式,再将得到的图象上各点的横坐标伸长到时原来的4倍,纵坐标不变,得到y=g(x)的解析式,分析[ ,2π]上,推出
,2π]上,推出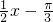 的范围,然后求出函数的最大值和最小值.
的范围,然后求出函数的最大值和最小值.点评:本题是中档题,考查三角函数的解析式的求法,周期的应用,三角函数的最值的求法,函数的平移变换,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
