题目内容
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数f(x)=ax2
(a>0),使得 (λ为常数),这里点P、Q的坐标分别为
(λ为常数),这里点P、Q的坐标分别为
P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
(a>0),使得
 (λ为常数),这里点P、Q的坐标分别为
(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
| A.(2,+∞) | B.(3,+∞) | C.[4,+∞) | D.[8,+∞) |
A
解:由题设知,点P(1,a),Q(k,ak2),A(5,0),
∴向量
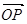 =(1,a),
=(1,a), 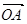 =(5,0),
=(5,0), 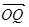 =(k,ak2),
=(k,ak2),∴
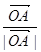 =(1,0),
=(1,0), 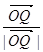 =(
=( 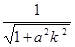 ,
,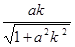 ),
),∵
 (λ为常数),.
(λ为常数),.∴1=λ(1+
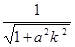 ),a=
),a= 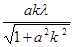 ,
,两式相除得,k-1=
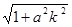 ,
,k-2=a2k>0
∴k(1-a2)=2,且k>2.
∴k=
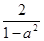 ,且0<1-a2<1.
,且0<1-a2<1.∴k=
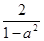 >2.
>2.故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
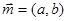 ,向量
,向量 ,向量p=(b-2,a-2)
,向量p=(b-2,a-2) ∥
∥ ,求证△ABC为等腰三角形;
,求证△ABC为等腰三角形; ,边长c=2,
,边长c=2, , 求 △ABC的面积.
, 求 △ABC的面积. 中,满足
中,满足 ,
, 是
是 中点.
中点. ,求向量
,求向量 与向量
与向量 的夹角的余弦值;
的夹角的余弦值; 是线段
是线段 上任意一点,且
上任意一点,且 ,求
,求 的最小值;
的最小值; 是
是 ,
, ,
, ,求
,求 的最小值.
的最小值. 中,
中, 分别为
分别为 的中点。设
的中点。设 ,用
,用 表示向量
表示向量
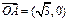 ,O为坐标原点,动点M满足:
,O为坐标原点,动点M满足: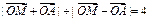 .
.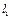 、
、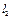 都过点
都过点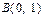 ,且
,且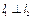 ,
,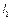 、
、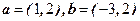 .
.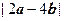 ;
;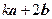 与
与 平行,求
平行,求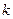 的值;
的值;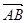 =a,
=a,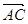 = b,则向量
= b,则向量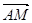 等于( )
等于( )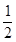 (a-b)
(a-b)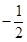 (a+b)
(a+b) 、
、 、
、 为空间的一个基底,则( )
为空间的一个基底,则( ) 中,
中, 是重心,
是重心, 过
过 ,若
,若 ,则
,则 .
.