题目内容
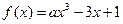 对于
对于 总有
总有 成立,则
成立,则 = 。
= 。4
本小题考查函数单调性及恒成立问题的综合运用,体现了分类讨论的数学思想。
要使 恒成立,只要
恒成立,只要 在
在 上恒成立。
上恒成立。

 当
当 时,
时, ,所以
,所以 ,不符合题意,舍去。
,不符合题意,舍去。
 当
当 时
时 ,即
,即 单调递减,
单调递减, ,舍去。
,舍去。
 当
当 时
时
① 若 时
时 在
在 和
和 上单调递增,
上单调递增,
在 上单调递减。
上单调递减。
所以

② 当 时
时 在
在 上单调递减,
上单调递减,
 ,不符合题意,舍去。综上可知a=4.
,不符合题意,舍去。综上可知a=4.
要使
 恒成立,只要
恒成立,只要 在
在 上恒成立。
上恒成立。
 当
当 时,
时, ,所以
,所以 ,不符合题意,舍去。
,不符合题意,舍去。 当
当 时
时 ,即
,即 单调递减,
单调递减, ,舍去。
,舍去。 当
当 时
时
① 若
 时
时 在
在 和
和 上单调递增,
上单调递增,在
 上单调递减。
上单调递减。所以


② 当
 时
时 在
在 上单调递减,
上单调递减, ,不符合题意,舍去。综上可知a=4.
,不符合题意,舍去。综上可知a=4.
练习册系列答案
相关题目
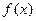 组成的:
组成的: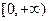 ;
; 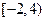 ;
;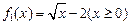 ,及
,及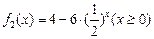 是否属于集合A?并简要说明理由.
是否属于集合A?并简要说明理由.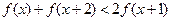 ,是否对于任意的
,是否对于任意的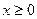 总成立?若不成立,为什么?若成立,请证明你的结论.
总成立?若不成立,为什么?若成立,请证明你的结论.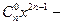
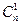
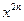
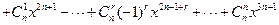 ,其中n
,其中n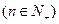 .
. (2)设函数f(x)取得极大值时x=
(2)设函数f(x)取得极大值时x=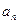 ,令
,令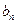 =2
=2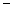 3
3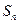 =
=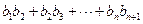 ,若p≤
,若p≤ 中,满足 “对
中,满足 “对 ,当
,当 时,都有
时,都有 ”的是
”的是 B.
B. C.
C. D.
D.
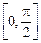 上的最大值为_________;在区间[0,2π]上最大值为___________.
上的最大值为_________;在区间[0,2π]上最大值为___________.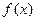 是
是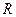 上的减函数,且
上的减函数,且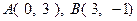 ,则当不等式
,则当不等式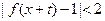 的解集为
的解集为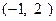 时,
时,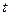 的值为
的值为 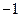
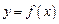
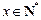
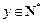
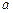 ,
,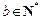 ,
,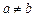 ,都有
,都有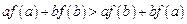 ;
;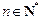 都有
都有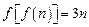 .
.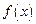 为
为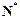 上的单调增函数;
上的单调增函数;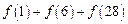 ;
;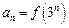 ,
,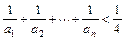
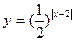 ,则它的单调区间为【 】.
,则它的单调区间为【 】.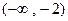 ,减区间为
,减区间为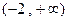
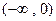 ,减区间为
,减区间为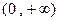
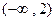 ,减区间为
,减区间为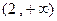
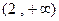 ,减区间为
,减区间为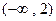
 的部分对应值如下表:
的部分对应值如下表: 的解集是 。
的解集是 。