题目内容
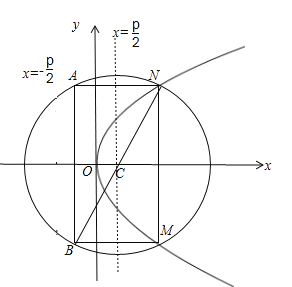
【题目】已知抛物线E:y2=2px(p>0)的准线为l,圆C:(x﹣![]() )2+y2=4,l与圆C交于A,B,圆C与E交于M,N.若A,B,M,N为同一个矩形的四个顶点,则E的方程为( )
)2+y2=4,l与圆C交于A,B,圆C与E交于M,N.若A,B,M,N为同一个矩形的四个顶点,则E的方程为( )
A. y2=xB. y2=![]() xC. y2=2xD. y2=2
xC. y2=2xD. y2=2![]() x
x
【答案】C
【解析】
由A,B,M,N为同一个矩形的四个顶点,可得点A,N关于直线x=![]() 对称,即
对称,即![]() ,可得|NA|=
,可得|NA|=![]() =2p,由抛物线定义得2p=2,可得E的方程.
=2p,由抛物线定义得2p=2,可得E的方程.
如图,圆C:(x﹣![]() )2+y2=4的圆心C(
)2+y2=4的圆心C(![]() ,0)是抛物线E:y2=2px(p>0)的焦点,
,0)是抛物线E:y2=2px(p>0)的焦点,
∵圆C:(x﹣![]() )2+y2=4的半径为2,
)2+y2=4的半径为2,
∴|NC|=2,根据抛物线定义可得:|NA|=|NC|=2.
∵A,B,M,N为同一个矩形的四个顶点,
∴点A,N关于直线x=![]() 对称,即
对称,即![]() ,∴
,∴![]() ,
,
∴|NA|=![]() =2,∴2p=2,则E的方程为y2=2x.
=2,∴2p=2,则E的方程为y2=2x.
故选:C.

 阅读快车系列答案
阅读快车系列答案【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.