题目内容
已知数列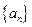 满足
满足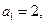 前
前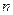 项和为
项和为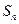 ,
,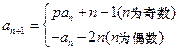 .
.
(1)若数列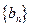 满足
满足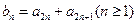 ,试求数列
,试求数列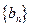 前3项的和
前3项的和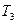 ;(4分)
;(4分)
(2)若数列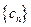 满足
满足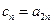 ,试判断
,试判断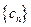 是否为等比数列,并说明理由;(6分)
是否为等比数列,并说明理由;(6分)
(3)当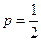 时,问是否存在
时,问是否存在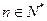 ,使得
,使得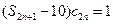 ,若存在,求出所有的
,若存在,求出所有的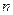 的值;
的值;
若不存在,请说明理由.(8分)
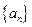 满足
满足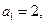 前
前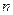 项和为
项和为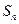 ,
,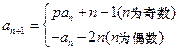 .
.(1)若数列
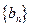 满足
满足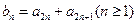 ,试求数列
,试求数列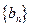 前3项的和
前3项的和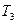 ;(4分)
;(4分)(2)若数列
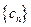 满足
满足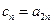 ,试判断
,试判断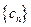 是否为等比数列,并说明理由;(6分)
是否为等比数列,并说明理由;(6分)(3)当
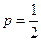 时,问是否存在
时,问是否存在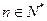 ,使得
,使得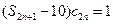 ,若存在,求出所有的
,若存在,求出所有的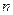 的值;
的值;若不存在,请说明理由.(8分)
解:(1)
据题意得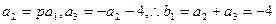 1分
1分
据题意得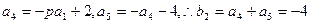 2分
2分
据题意得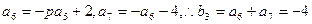 3分
3分
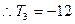 4分
4分
(2)(理)当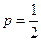 时,数列
时,数列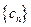 成等比数列; 5分
成等比数列; 5分
当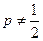 时,数列
时,数列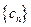 不为等比数列 6分
不为等比数列 6分
理由如下:因为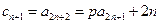
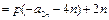
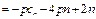 , 7分
, 7分
所以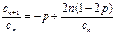 , 8分
, 8分
故当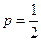 时,数列
时,数列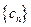 是首项为1,公比为
是首项为1,公比为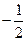 等比数列; 9分
等比数列; 9分
当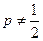 时,数列
时,数列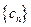 不成等比数列 10分
不成等比数列 10分
(文)因为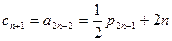 6分
6分
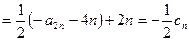 8分
8分
所以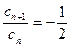 9分
9分
故当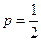 时,数列
时,数列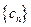 是首项为1,公比为
是首项为1,公比为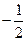 等比数列; 10分
等比数列; 10分
(3)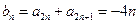 ,所以
,所以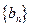 成等差数列,
成等差数列,  11分
11分
当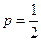 时
时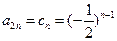 , 12分
, 12分
因为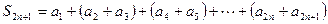
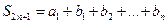 =
=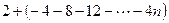
=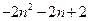 (
(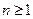 ) 13分
) 13分
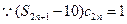 ,
,
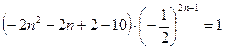
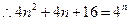 , 14分
, 14分
设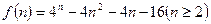 ,
,
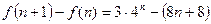
=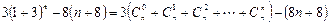
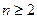 时
时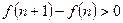 ,所以
,所以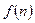 在
在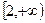 递增 17分
递增 17分
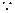
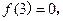
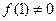 ,
,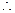 仅存
仅存 在惟一的
在惟一的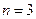 使得
使得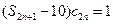 成立 18分
成立 18分
据题意得
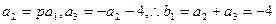 1分
1分据题意得
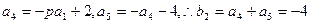 2分
2分据题意得
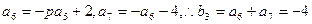 3分
3分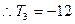 4分
4分(2)(理)当
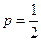 时,数列
时,数列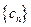 成等比数列; 5分
成等比数列; 5分当
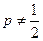 时,数列
时,数列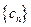 不为等比数列 6分
不为等比数列 6分理由如下:因为
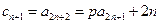
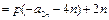
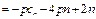 , 7分
, 7分所以
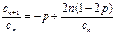 , 8分
, 8分故当
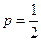 时,数列
时,数列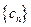 是首项为1,公比为
是首项为1,公比为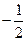 等比数列; 9分
等比数列; 9分当
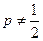 时,数列
时,数列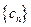 不成等比数列 10分
不成等比数列 10分(文)因为
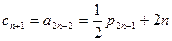 6分
6分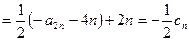 8分
8分所以
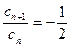 9分
9分故当
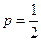 时,数列
时,数列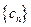 是首项为1,公比为
是首项为1,公比为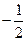 等比数列; 10分
等比数列; 10分(3)
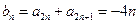 ,所以
,所以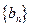 成等差数列,
成等差数列,  11分
11分当
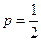 时
时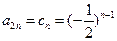 , 12分
, 12分因为
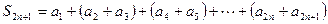
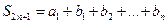 =
=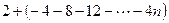
=
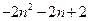 (
(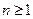 ) 13分
) 13分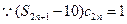 ,
,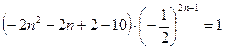
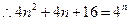 , 14分
, 14分设
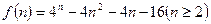 ,
,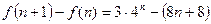
=
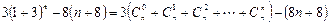
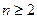 时
时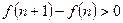 ,所以
,所以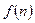 在
在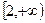 递增 17分
递增 17分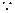
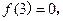
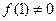 ,
,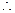 仅存
仅存 在惟一的
在惟一的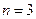 使得
使得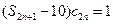 成立 18分
成立 18分略

练习册系列答案
相关题目
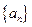 是等差数列,其中
是等差数列,其中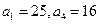
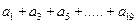 值。
值。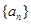 满足
满足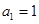 ,
,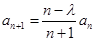 ,其中
,其中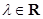 ,
,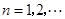 .
.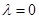 时,
时,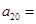 _____;
_____;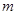 ,当
,当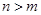 时总有
时总有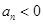 ,则
,则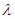 的取值范围是_____.
的取值范围是_____.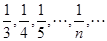 中第10项是 ( )
中第10项是 ( )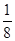
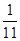
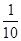
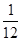
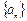 中,如果
中,如果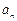 =3n(n=1,2
=3n(n=1,2 ,3,…) ,那么这个数列是 ( )
,3,…) ,那么这个数列是 ( )
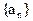 为等差数列,
为等差数列,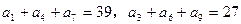 ,则
,则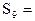 __________
__________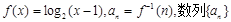 的前
的前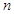 项和为
项和为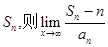 等于
等于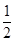
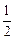 a3、a1成等差数列,则
a3、a1成等差数列,则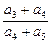 = ▲ .
= ▲ . 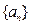 ,
,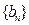 的前
的前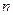 项和分别为
项和分别为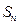 ,
,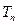 ,若
,若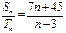 ,则使
,则使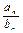 为整数的正整数n的取值个数是( )
为整数的正整数n的取值个数是( )