题目内容
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出![]() 的极坐标方程和
的极坐标方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 和
和![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,射线
两点,射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,射线
,射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
【答案】(1)线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)(1)利用cos2θ+sin2θ=1,即可曲线C1的参数方程化为普通方程,进而利用![]() 即可化为极坐标方程,同理可得曲线C2的直角坐标方程;
即可化为极坐标方程,同理可得曲线C2的直角坐标方程;
(2)由![]() 过
过![]() 的圆心,得
的圆心,得![]() 得
得![]() ,设
,设![]() ,
,![]() ,
,![]() 代入
代入![]() 中即可得解.
中即可得解.
试题解析:
(1)曲线![]() 的普通方程为
的普通方程为![]() ,化成极坐标方程为
,化成极坐标方程为![]()
曲线![]() 的直角坐标方程为
的直角坐标方程为![]()
(2)在直角坐标系下,![]() ,
,![]() ,
,![]()
恰好过![]() 的圆心,
的圆心,
∴![]() 由
由![]() 得
得![]()
![]() ,
,![]() 是椭圆
是椭圆![]() 上的两点,
上的两点,
在极坐标下,设![]() ,
,![]() 分别代入
分别代入![]() 中,
中,
有![]() 和
和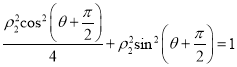
∴![]() ,
,![]()
则![]() ,即
,即![]()

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 | 90.10% | 4.98% | 3.82% | 1.10% |
净利润占比 | 95.80% |
| 3.82% | 0.86% |
则下列判断中不正确的是( )
A.该公司2018年度冰箱类电器销售亏损
B.该公司2018年度小家电类电器营业收入和净利润相同
C.该公司2018年度净利润主要由空调类电器销售提供
D.剔除冰箱类销售数据后,该公司2018年度空调类电器销售净利润占比将会降低