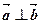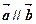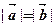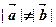题目内容
已知⊙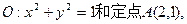 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足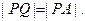
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程
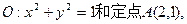 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足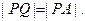
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程
(1)
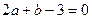
(2)
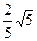
(3)
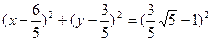
解:(1)连OP,
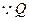 为切点,PQ⊥OQ,由勾股定理有
为切点,PQ⊥OQ,由勾股定理有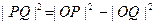
由已知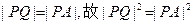
即: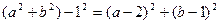
化简得实数a、b间满足的等量关系为:
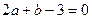
(2)由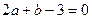 ,得b=-2a+3 。
,得b=-2a+3 。
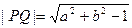
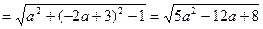
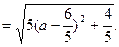
故当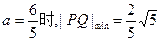 ,即线段PQ长的最小值为
,即线段PQ长的最小值为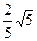
(3)设⊙P的半径为R,
OP设⊙O有公共点,⊙O的半径为1,
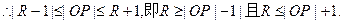
而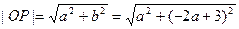
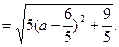
故当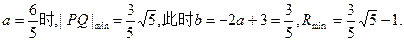
得半径取最小值⊙P的方程为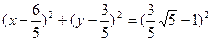
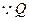 为切点,PQ⊥OQ,由勾股定理有
为切点,PQ⊥OQ,由勾股定理有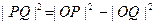
由已知
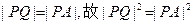
即:
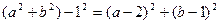
化简得实数a、b间满足的等量关系为:
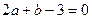
(2)由
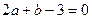 ,得b=-2a+3 。
,得b=-2a+3 。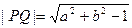
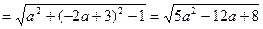
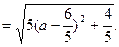
故当
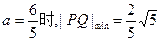 ,即线段PQ长的最小值为
,即线段PQ长的最小值为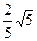
(3)设⊙P的半径为R,
OP设⊙O有公共点,⊙O的半径为1,
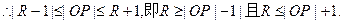
而
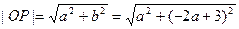
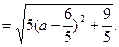
故当
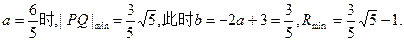
得半径取最小值⊙P的方程为
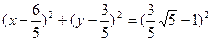

练习册系列答案
相关题目
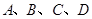 是空间不共面的四点,且满足
是空间不共面的四点,且满足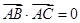 ,
, ,
,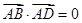 ,则
,则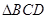 是( )
是( )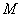 是线段
是线段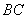 的中点,点
的中点,点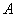 在直线
在直线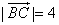 ,
,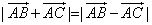 ,则
,则 ________
________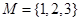 ,
,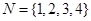 ,定义函数
,定义函数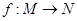 . 若点
. 若点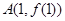 ,
,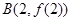 ,
,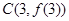 ,
,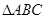 的外接圆圆心为D,且
的外接圆圆心为D,且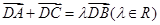 ,则满足条件的函数
,则满足条件的函数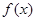 有( )
有( ) ,设
,设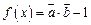
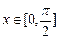 ,求
,求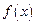 的值域.
的值域.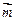 平移后得到
平移后得到 的图象,指出向量
的图象,指出向量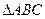 的面积是30,内角
的面积是30,内角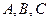 所对边长分别为
所对边长分别为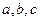 ,
,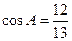 。
。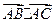 ;
;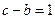 ,求
,求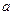 的值。
的值。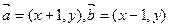 ,点
,点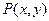 为动点,
为动点, 已知
已知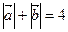 。
。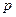 的轨迹方程;
的轨迹方程;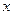 轴负半轴交于点
轴负半轴交于点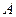 ,过点
,过点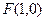 的直线交点
的直线交点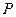 的轨迹于
的轨迹于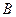 、
、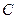 两点,试推断
两点,试推断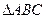 的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。
的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。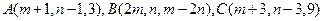 三点共线,则
三点共线,则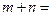 .
.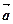 ,
,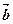 是非零向量,若函数
是非零向量,若函数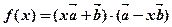 的图象是一条直线,则必有
的图象是一条直线,则必有