题目内容
在△ABC中,角A,B,C所对的边分别为 ,已知函数
,已知函数
 R).
R).
(Ⅰ)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(Ⅱ)若函数 在
在 处取得最大值,且
处取得最大值,且 ,求
,求 的面积
的面积 .
.
(Ⅰ)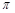 ,
,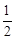 ;(Ⅱ)
;(Ⅱ)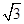 .
.
解析试题分析:(Ⅰ)利用三角函数公式把函数 化简为一个角的三角函数,从而易得函数
化简为一个角的三角函数,从而易得函数 的最小正周期和最大值;(Ⅱ)由(Ⅰ)函数先求角A,再由向量数量积公式求
的最小正周期和最大值;(Ⅱ)由(Ⅰ)函数先求角A,再由向量数量积公式求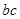 的值,从而利用
的值,从而利用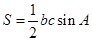 求得三角形面积.
求得三角形面积.
试题解析:(Ⅰ)依题意,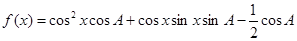 2分
2分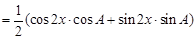
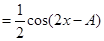 5分
5分
所以函数 的最小正周期是
的最小正周期是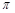 ,
, 有最大值
有最大值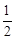 . 7分
. 7分
(Ⅱ)由(I)知:由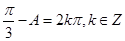 ,得
,得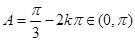 , 所以
, 所以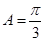 .
.
又 ,所以
,所以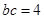 .
.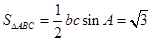 . 14分
. 14分
考点:1、三角函数的性质;2、向量的数量积;3、正弦定理.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
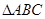 中,
中,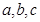 分别为角
分别为角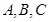 的对边,
的对边,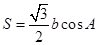
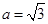 ,设角B的大小为x,用x表示c,并求c的取值范围.
,设角B的大小为x,用x表示c,并求c的取值范围. .
.
 的最小值及取最小值时
的最小值及取最小值时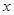 的集合;
的集合;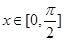 时的值域;
时的值域;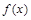 在区间
在区间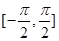 上的图像(要求列表,描点).
上的图像(要求列表,描点).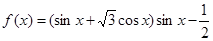 .
. 的单调递减区间;
的单调递减区间;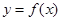 的图像向左平移
的图像向左平移 个单位,再将得到的图像横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图像横坐标变为原来的2倍(纵坐标不变)后得到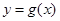 的图像,若
的图像,若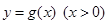 的图像与直线
的图像与直线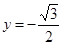 交点的横坐标由小到大依次是
交点的横坐标由小到大依次是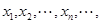 求数列
求数列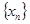 的前2n项的和。
的前2n项的和。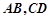 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9
的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9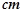 和15
和15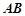 的顶部
的顶部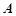 看建筑物
看建筑物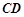 的视角
的视角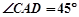 .
.
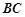 的长度;
的长度;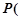 点
点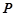 与点
与点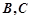 不重合),从点
不重合),从点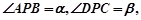 问点
问点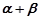 最小?
最小? 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, 的值;
的值; ,
, ,求
,求 的值.
的值.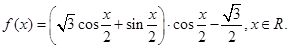
 的最小正周期;
的最小正周期; 的内角A、B、C的对边分别为
的内角A、B、C的对边分别为 ,若
,若 且
且 ,求角B的值.
,求角B的值.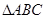 中,角
中,角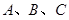 所对的边为
所对的边为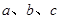 ,且满足
,且满足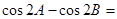
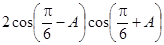
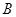 的值;
的值;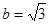 且
且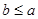 ,求
,求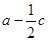 的取值范围.
的取值范围.