题目内容
数列{an}的前n项为Sn=n2+2n，则此数列的通项公式为 ．
考点：数列的函数特性
专题：等差数列与等比数列
分析：当n=1时，S1=3，
根据当n≥2时，an=Sn-Sn-1，代入求解即可．
根据当n≥2时，an=Sn-Sn-1，代入求解即可．
解答：
解：∵数列{an}的前n项为Sn=n2+2n，
∴当n=1时，S1=3，
当n≥2时，an=Sn-Sn-1=n2+2n-（n-1）2-2（n-1）=2n+1，n≥2，
n=1，符合题意
∴此数列的通项公式为an=2n+1，
∴当n=1时，S1=3，
当n≥2时，an=Sn-Sn-1=n2+2n-（n-1）2-2（n-1）=2n+1，n≥2，
n=1，符合题意
∴此数列的通项公式为an=2n+1，
点评：本题考查了数列的前n项和，通项公式的函数性，属于容易题，关键是容易漏掉n=1．
练习册系列答案
相关题目
将函数y=cos（x-
）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得图象向左平移
个单位，则所得函数具有性质是（ ）
| 5π |
| 6 |
| π |
| 3 |
A、图象关于直线x=
| ||
B、图象关于(
| ||
C、图象关于直线x=
| ||
D、图象关于(
|
数列{an}的前n项和Sn=3n2+3n（n∈N*），bn=lg
（n∈N*），则数列{bn}的前99项和T99=（ ）
| an+1 |
| an |
| A、6 | B、2 |
| C、lg99 | D、3lg99 |
已知命题p：a＜0时方程ax2+2x+1=0至少有一个负数根（ ）
| A、￢p是真命题 |
| B、p的逆命题是真命题 |
| C、p的否命题是真命题 |
| D、p的逆否命题是真命题 |
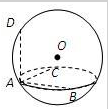如图，设ABCD内球O上的四个点，若AB，AC，AD两两互相垂直，且AB=1，AC=2，AD=2，则此球的体积为