题目内容
数列{an}的前n项和Sn=3n2+3n（n∈N*），bn=lg
（n∈N*），则数列{bn}的前99项和T99=（ ）
| an+1 |
| an |
| A、6 | B、2 |
| C、lg99 | D、3lg99 |
考点：数列的求和
专题：等差数列与等比数列
分析：数列{an}的前n项和Sn=3n2+3n（n∈N*），当n≥2时，an=Sn-Sn-1=6n．当n=1时，a1=6．可得an=6n．于是bn=lg
=lg（n+1）-lgn（n∈N*），利用“累加求和”即可得出数列{bn}的前99项和T99．
| an+1 |
| an |
解答：
解：∵数列{an}的前n项和Sn=3n2+3n（n∈N*），
∴当n≥2时，an=Sn-Sn-1=3n2+3n-[3（n-1）2+3（n-1）]=6n．
当n=1时，a1=6，上式也成立．
∴an=6n．
∴bn=lg
=lg（n+1）-lgn（n∈N*），
则数列{bn}的前99项和T99=（lg2-lg1）+（lg3-lg2）+…+（lg100-lg99）=lg100-lg1=2．
故选：B．
∴当n≥2时，an=Sn-Sn-1=3n2+3n-[3（n-1）2+3（n-1）]=6n．
当n=1时，a1=6，上式也成立．
∴an=6n．
∴bn=lg
| an+1 |
| an |
则数列{bn}的前99项和T99=（lg2-lg1）+（lg3-lg2）+…+（lg100-lg99）=lg100-lg1=2．
故选：B．
点评：本题考查了递推式的应用、“累加求和”、对数的运算性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
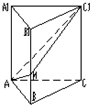如图，直三棱柱ABC-A1B1C1中，AB=1，BC=2，AC=