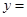题目内容
已知函数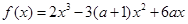
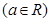 .
.
(1)当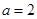 时,求函数
时,求函数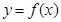 的单调区间;
的单调区间;
(2)若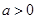 时,函数
时,函数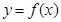 在闭区间
在闭区间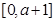 上的最大值为
上的最大值为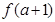 ,求
,求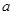 的取值范围.
的取值范围.
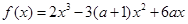
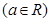 .
.(1)当
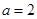 时,求函数
时,求函数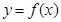 的单调区间;
的单调区间;(2)若
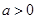 时,函数
时,函数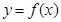 在闭区间
在闭区间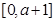 上的最大值为
上的最大值为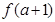 ,求
,求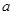 的取值范围.
的取值范围.(1)单调增区间分别为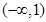 ,
,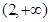 ,单调减区间为
,单调减区间为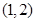 ;(2)
;(2)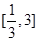 .
.
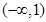 ,
,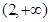 ,单调减区间为
,单调减区间为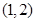 ;(2)
;(2)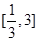 .
.试题分析:本题主要考查导数的运算,利用导数研究函数的单调性、极值、最值以及不等式的基础知识,考查分类讨论思想,考查综合运用数学知识和方法分析问题解决问题的能力和计算能力.第一问,当
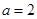 时,函数解析式中没有参数,直接求导,令导数大于0和小于0,分别解出函数的单调增区间和单调减区间;第二问,因为
时,函数解析式中没有参数,直接求导,令导数大于0和小于0,分别解出函数的单调增区间和单调减区间;第二问,因为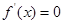 的两个根是
的两个根是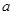 和1,所以需要讨论
和1,所以需要讨论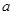 和1的大小,分3种情况进行讨论,分别列表判断函数的单调性、极值、最值,求出函数在闭区间
和1的大小,分3种情况进行讨论,分别列表判断函数的单调性、极值、最值,求出函数在闭区间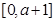 上的最大值判断是否等于
上的最大值判断是否等于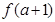 ,求出
,求出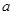 的取值范围.
的取值范围.试题解析:
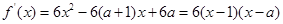 2分
2分(1)当
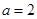 时,
时,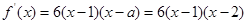
当
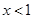 或
或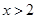 时,
时,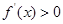 ,
, 当
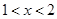 ,
,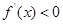 ,
,所以
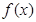 的单调增区间分别为
的单调增区间分别为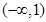 ,
,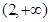 , 5分
, 5分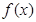 的单调减区间为
的单调减区间为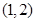 .
.(2)(Ⅰ)当
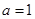 时,
时, ,
,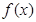 在
在 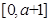 上单调递增,最大值为
上单调递增,最大值为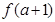
(Ⅱ)当
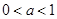 时,列表如下:
时,列表如下:| x | 0 | (0,a) | a | (a,1) | 1 | (1,1+a) | a+1 |
| f/(x) | | + | 0 | - | 0 | + | |
| f(x) | | 增 | 极大值f(a) | 减 | | 增 | |
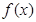 在
在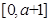 上的最大值,只有可能是
上的最大值,只有可能是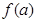 或
或 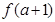
所以只需

解得
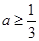 ,此时
,此时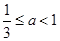 .
.(Ⅲ)当
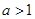 时,列表如下:
时,列表如下:| x | 0 | (0,1) | 1 | (1 ,a) | a | (a,1+a) | a+1 |
| f/(x) | | + | 0 | - | 0 | + | |
| f(x) | | 增 | 极大值f(1) | 减 | | 增 | |
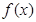 在
在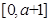 上的最大值,只有可能是
上的最大值,只有可能是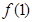 或
或 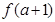
所以只需
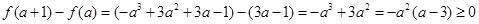
解得
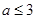 ,此时
,此时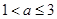 . 11分
. 11分由(Ⅰ)(Ⅱ)(Ⅲ)得
 ,
,所以满足条件的
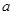 的取值范围是
的取值范围是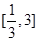 . 12分
. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
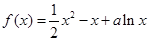 (其中
(其中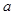 为常数).
为常数).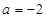 时,求函数
时,求函数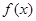 的最值;
的最值;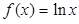 .
.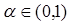 ,求
,求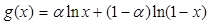 最大值;
最大值;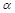 ,
,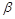 满足
满足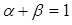 .求证:
.求证: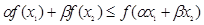 ;
;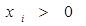 ,正数
,正数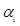 满足
满足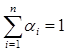 .证明:
.证明: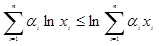
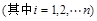 .
. 满足
满足 ,且
,且 为偶函数,当
为偶函数,当 时,有( )
时,有( )



 是定义在R上的可导函数,当x≠0时,
是定义在R上的可导函数,当x≠0时, ,则关于x的函数
,则关于x的函数
 的零点个数为( )
的零点个数为( )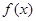 ,对任意x都有
,对任意x都有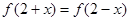 ,且其导函数
,且其导函数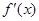 满足
满足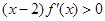 ,则当
,则当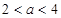 时,有( )
时,有( )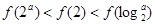
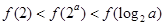
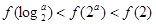
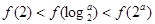
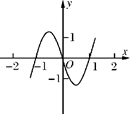
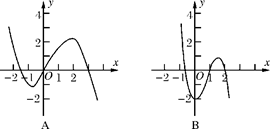
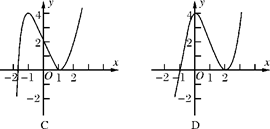
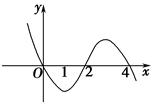
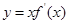 的图象如图所示(其中
的图象如图所示(其中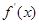 是函数
是函数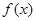 的导函数)下面四个图象中,
的导函数)下面四个图象中,