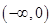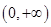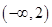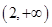题目内容
已知函数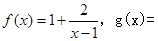 f(2x)
f(2x)
(I)用定义证明函数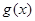 在
在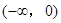 上为减函数。
上为减函数。
(II)求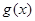 在
在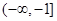 上的最小值.
上的最小值.
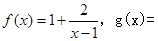 f(2x)
f(2x)(I)用定义证明函数
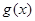 在
在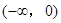 上为减函数。
上为减函数。(II)求
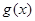 在
在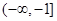 上的最小值.
上的最小值.(I)见解析(II)-3
试题分析:(I)先求出
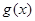 的解析式,再根据函数单调性的定义证明:第一步,在所给区间内任取两个自变量的值
的解析式,再根据函数单调性的定义证明:第一步,在所给区间内任取两个自变量的值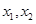 且
且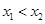 ;第二步,比较
;第二步,比较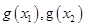 的大小;第三步,下结论.
的大小;第三步,下结论.(II)利用函数单调性
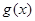 在
在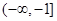 的单调性求出最小值.
的单调性求出最小值.试题解析:解:(I)
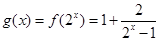
又
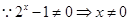 ∴函数
∴函数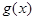 的定义域
的定义域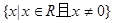 , 3分
, 3分设
 且
且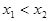
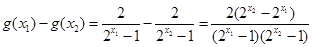 6分
6分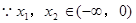 且
且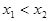 ,
,∴
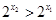 且
且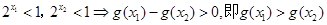
根据函数单调性的定义知:函数
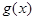 在
在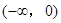 上为减函数. 8分
上为减函数. 8分(II)∵ :函数
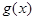 在
在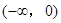 上为减函数,∴:函数
上为减函数,∴:函数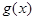 在
在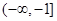 上为减函数,
上为减函数,∴当x=-1时,
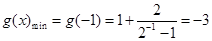 12分
12分
练习册系列答案
相关题目
 是定义在(-1,1)上的奇函数,其中
是定义在(-1,1)上的奇函数,其中 ,a为正整数,且满足
,a为正整数,且满足 .
. 的解析式;
的解析式; 的
的 的范围;
的范围; ),f(-1)的大小关系为( )
),f(-1)的大小关系为( )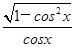 ( ).
( ). 上递增
上递增 上递增,在
上递增,在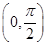 上递减
上递减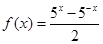 ( )
( )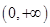 上是减函数
上是减函数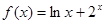 , 若
, 若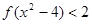 , 则实数
, 则实数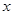 的取值范围 .
的取值范围 .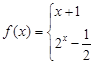
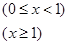 ,设
,设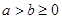 ,若
,若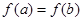 ,
,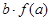 的取值范围是( )
的取值范围是( )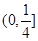
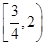
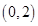
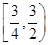
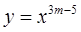 ,其中
,其中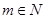 ,且在
,且在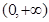 上是减函数,又
上是减函数,又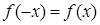 ,则
,则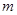 =( )
=( )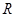 上的可导函数
上的可导函数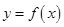 的导函数为
的导函数为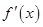 ,满足
,满足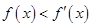 ,且
,且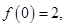 则不等式
则不等式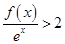 的解集为( )
的解集为( )